- It's Week 5: the weeks fly
by. This week we're featuring another analytic integration
technique, and then numerical integration (when all else
fails).
- A snow day! Who would have thought it. If you were not able to
come to Tuesday lab, because of the University closure, and
would like to come Thursday, let me know. We certainly have
some spaces open on Thursday.
First come, first served -- I'll take the first 8 who respond. Otherwise you'll have to zoom it.
- Your Weekly homework #3 is due tonight (Wednesday). I pushed it
back, because I'm grading other things and can't get to it
before then anyway.
- You do have a new Weekly assignment #4. It is due next Wednesday.
- What's integration all about? Well, we usually start by going
about calculating (signed) areas (which means that areas can be
negative):
\[ A=\int{dA} \]
"dA" is called an "infinitesimal" -- it's a tiny chunk of area -- tinier than anything you know ("vanishingly small")!
What's numerical integration all about? We do pretty much the same thing, only we have a finite sum \[ A=\sum{\Delta {A}} \]
where the $\Delta {A}$ are small, but not vanishingly small. And our favorite little areas are rectangles.
- There are times when we cannot find an explicit anti-derivative function
for an integrand, and hence we are obliged to resort to numerical methods:
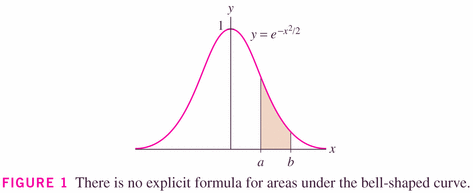
- There are various schemes for numerical integration (and it turns
out that each one of these relies on breaking that smooth area above
into rectangles!):
- Left-endpoint Rectangle Rule.
- Right-endpoint Rectangle Rule.
- Midpoint Rule.
- Trapezoidal Rule.
- Simpson's Rule.
- Three of the rules are so called "rectangle rules" (LRR, RRR, Midpoint Rule);
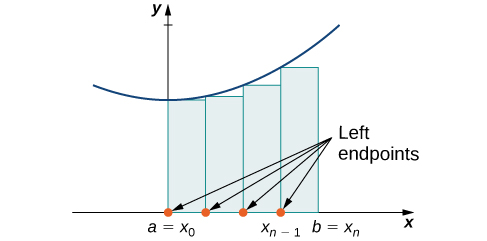
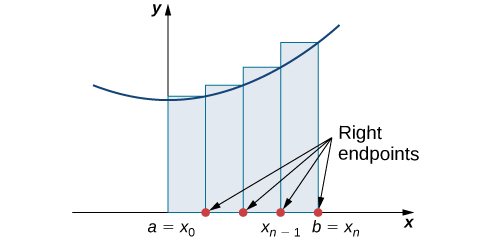
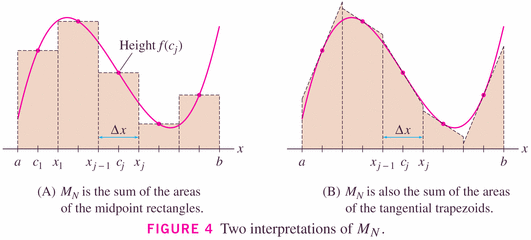
but as the image to the right (above) and the graphical insight below show, we can think of the Midpoint rule as being a "Tangent rule":
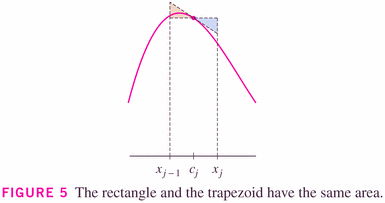
Midpoint Rule: \[ \int_a^b f(x) dx \approx M_n = \Delta x [f(\overline{x_1})+f(\overline{x_2})+\cdots+f(\overline{x_n})] \] where \[ \Delta x = \frac{b-a}{n} \] and $\overline{x_i}=\frac{1}{2}(x_{i-1}+x_i)=$ midpoint of $[x_{i-1},x_i]$.
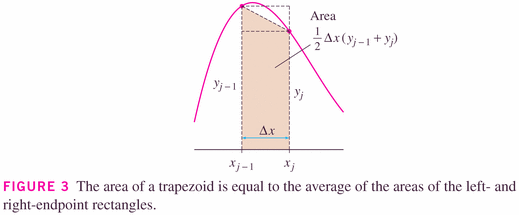
- The Trapezoidal rule is really just the average of the Left- and
Right-rectangle Rules:
This gives rise to an important observation, which I want to encourage you to remember, and here it is:
When you have two estimates, you have a third. (their arithmetic average, in this case). Notice that the two methods (LRR and RRR) make errors in the opposite sense in this case (and generally): one method tends to overestimate (the left, in this case), while the other tends to underestimate (RRR here); the average cancels their errors, to produce a more accurate estimate (in general).
Trapezoidal Rule: \[ \int_a^b f(x) dx \approx T_n = \frac{\Delta x}{2} [f(a)+2f(x_1)+2f(x_2)+\cdots+2f(x_{n-1})+f(b)] \] where \[ \Delta x = \frac{b-a}{n} \] and $x_i=a + i \Delta x$. This is just the average of the RRR and LRR: \[ LRR = \Delta x [f(a)+f(x_1)+f(x_2)+\cdots+f(x_{n-1})] \] \[ RRR = \Delta x [f(x_1)+f(x_2)+\cdots+f(x_{n-1})+f(b)] \] (and note that each of those methods ignores one endpoint).
Be careful however not to confuse the midpoint and trapezoidal rule. Each is effectively a trapezoid method, but the midpoint method uses "tangent trapezoids", while the trapezoid method uses "endpoint trapezoids" (and it turns out that the tangent trapezoids give better results, generally).

- Simpson's rule is a "blend" (or weighted average) of the Midpoint
and Trapezoidal rules, which perfectly balances the errors of the two
to generate a better rule:
\[
S_{2n}=\frac{2M_{n}+T_{n}}{3}
\]
Notice that the number of subintervals in Simpson's rule must be even.
Now we can go further:
When you have two estimates, you have infinitely many more. (their weighted arithmetic averages).
Here are the error bounds, that illustrate that the errors of midpoint and trapezoidal are related, and suggest how to combine them to create a better method (Simpson's rule):


Notice that we're adding two copies of the Midpoint rule to one copy of the Trapezoidal rule -- so Simpson's rule has three estimates of the integral in the numerator (so we must divide that by 3 to produce a single estimate, Simpson's rule). Because the error of the Trapezoidal rule tends to be about twice the error of the Midpoint rule, and of opposite sign, the errors cancel in a beautiful way to create a cool new rule!
- Here's a nice summary of the issue, focused on the use of Mathematica to illustrate them. Interesting even if you don't use Mathematica.
- Numerical Integration on-line.
- Here is a hand out which emphasizes this message. Let's take a look at this:
- Mathematica code
- Check midpoint calculation
- Let's do the calculations by the formulas, for
- Trapezoid
- Simpson's
- Check that we get the same things using the averages
- Calculate the true value of the integral, and compare to the approximations. What's surprising?