- Zoom:
- Start it.
- Share screen.
- Record.
- Make sure everyone can hear remotely.
- We're in lucky week 13; hopefully
you were able to relax a little over our "long
weekend", and get rested up for the sprint to the end
of the semester.
Next weekend we have one more midterm exam, and still a fair amount of new material yet to encounter.
We're finishing up series, with Taylor series (the extension of Taylor Polynomials); so that's both old and new. It's the focus of today's lab.
Then it will be on to parametric and polar equations; extensions of these to three-space (curves in three dimensions); vectors in two and three dimensions; and finally lines and planes in space (3D).
- Details on your exams were shared in Monday's
materials.
If you have questions or concerns, please contact me.
- Your colleague Yimin found a problem with one of the IMath problems, in 11.9, and so I withdrew it. But I saved the work we did, so that you can check it out. It was #11.
- We've seen that we can represent functions pretty well as Taylor
polynomials. But why stop at $n$?
- Power series suggest that we can just keep on going with those
Taylor polynomials, all the way to infinity -- and it's
true. And the strategy will be the same (with some of the new
questions asked of power series, which weren't an issue with
those finite polynomials):
- At what value $x=a$ should we center this infinite polynomial?
- For coefficients, we'll continue to choose them to match higher and higher derivatives of the function at that particular center $x=a$ -- we might say that we fit the function "infinitely well" at $a$.
- Then for what values will this particular power series be valid? Over what domain is the power series actually equal to the function?
- And, in particular, what happens on the boundary of that domain if it's finite?
In materials last time I mentioned an important example: the "geometric series" function, \[ f(x) = \frac{1}{1-x} ``=" \sum_{n=0}^\infty x^n \] (where $x$ plays the role that we've been having $r$ play).
On the right is a power series, expanded about $x=0$; and clearly it is "equal" to the function on the left -- but only sometimes. So this is a bit of a curious thing: why is it only valid on a small "radius" around 0 -- what we call the radius of convergence?
Obviously bad things happen to both the function and the power series when we get to $x=1$: both explode. But bad things also happen to the power series when we get to $x=-1$: an alternating series of ones, which doesn't converge. Yet $f(-1)=\frac{1}{2}$ -- perfectly well behaved.
We say that the radius of convergence of the series is 1, and the interval of convergence is $(-1,1)$ -- open -- to reflect the fact that the boundary values don't "work".
But why is it called a "radius"?
For the answer to that, we have to wander into the complex plane. If anyone ever asks you "What's the point in talking about imaginary numbers?" -- well, you're going to have an answer for them soon!
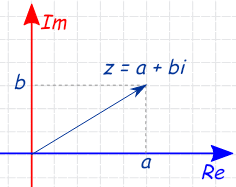
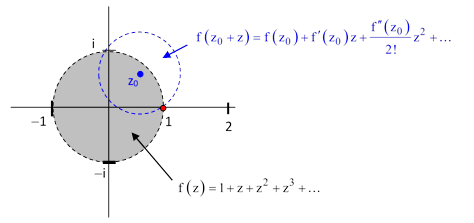
So this explains why we call it a "radius" of convergence: because it's actually the radius of a circle. There's a circle in the complex plane, of radius 1, and the power series serves perfectly well as $f$ for any complex number within that circle (centered at $z=x=0$).
- But the real reason I wanted to bring up the complex plane
is to talk about another remarkable formula.
Last week I shared Ramanujan's remarkable formula, \[ 1 + 2 + 3 + 4 + \ldots = -\frac{1}{12} \]
That might have made your head spin (as it did mine).
This week's remarkable formula is due to Euler (called "Euler's formula"), and looks like this: \[ e^{i\theta} = \cos{\theta} + i \sin{\theta} \]
What on earth is the exponential function $e^x$ doing fraternizing with the "circular functions" $\sin(x)$ and $\cos(x)$?
But we can use Taylor series to see that this formula is true. What's the Taylor series for $e^x$? Another remarkable series, which we encountered in Monday's materials:
\[ e^x=\sum_{n=0}^\infty\frac{x^n}{n!} =1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + \ldots \]
This series makes sense, because if you differentiate it term-by-term, you get the same series back:
\[ \left(e^x\right)'= 0 + 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + \ldots = e^x \]
Furthermore, it has a radius of convergence of $\infty$. It converges everywhere (in the complex plane, too!), as the ratio test shows:
\[ \lim_{n\to\infty} \left|\frac{\frac{x^{n+1}}{(n+1)!}}{\frac{x^n}{n!}}\right| = \lim_{n\to\infty} \left|\frac{x}{n+1}\right| = 0 \]
Plug in $x=i\theta$:
\[ e^{i\theta}=\sum_{n=0}^\infty\frac{(i\theta)^n}{n!} = \sum_{n=0}^\infty\frac{i^n\theta^n}{n!} \]
Now the key is that it's easy to compute power of $i$: \[ \begin{array}{cc} {i^0=1}\cr {i^1=i}\cr {i^2=-1}\cr {i^3=-i}\cr {i^4=1} \end{array} \]
So odd power are imaginary, and even powers are real. And signs alternate. So let's split the series into the two parts, even and odd, distributing out the $i$ from the odd terms, and we get this:
\[ e^{i\theta}= \sum_{n=0}^\infty(-1)^n\frac{\theta^{2n}}{(2n)!} + i\sum_{n=0}^\infty(-1)^n\frac{\theta^{2n+1}}{(2n+1)!} \]
Turns out that those two series on the right are the Taylor series for cosine and sine! Imagine (ary)! Therefore
\[ e^{i\theta}= \cos(\theta) + i\sin(\theta) \]
So the exponential function has an intimate relationship with the trig functions sine and cosine. We just have to wander into the complex plane to see it.
All this and more awaits you, if you'll only take complex analysis...:)
A couple of notes:
- the reason we can rearrange the terms in the power series is because the series is absolutely convergent.
- We can use a particular value of $\theta$ to write "Euler's
Equation", considered by some the most beautiful equation in
all of mathematics:
\[
e^{i\pi}=
\cos(\pi)
+
i\sin(\pi)
=
-1
+
0
\]
so
\[
\huge e^{i\pi} + 1 = 0
\]
Euler's equation: the most beautiful equation in mathematics.... or is it?
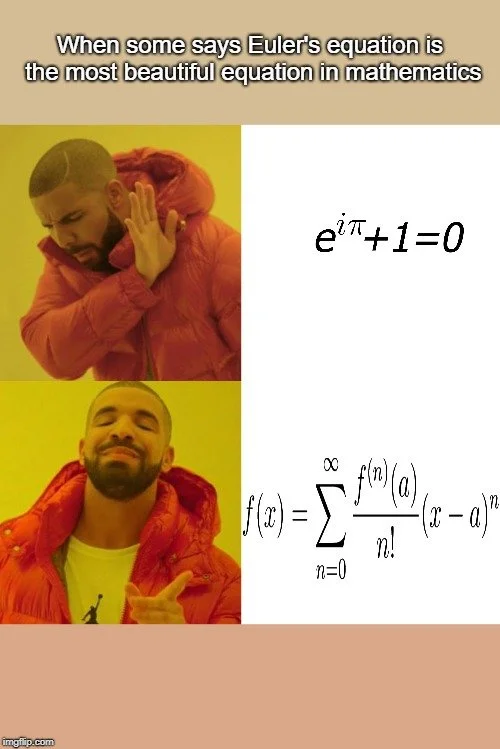
- Materials:
- The Riemann
series theorem: if an infinite series of real numbers is
conditionally convergent, then its terms can be arranged in a
permutation so that the new series converges to an arbitrary real
number, or diverges.