- Your quiz today is over infinity.
- I've added a couple of videos to our assignment page that go over
some of these paradoxes.
- No quiz next week: we'll just review for the final.
- Reminder: we're just days from our project and logo demonstrations (the last week of
class).
We'll do logos on Monday, and projects on Tuesday. If you have any conflicts on those days, let me know in advance. You are expected to attend to support your classmates. Please be on time.
I'll want your digital materials in advance. Please get those to me by Sunday evening (logos), and by Monday evening (projects). Anything that we'll want to display, so that I can have it ready to go.
If you want to go early in the presentations, let me know. Otherwise, your presentations will be ordered randomly (although I'll have prepared the order in advance, with the materials lined up).
You'll have three minutes for your presentation. You should talk about the logo/project itself, your motivation or what it means to you, and about the particular mathematics involved. You should definitely have three minutes of material -- make me cut you off!
At the end of class, you'll be asked to give me some positive comments about three of the presentations that resonated with you. These will be shared (anonymously) with the presenters at a later date.
- We revisited our work with Pascal's triangle, and its backwards
formulation, leading to that very strange formula
\[
S = 1+2+3+4+5+6+7+8+\ldots = -\frac{1}{12}
\]
- Only 150 years ago, mathematicians thought that infinity was a
single amorphous thing. Then Georg Cantor came along....
- The ping-pong ball conundrum is a popularization of the Ross-Littlewood
paradox, which was known by 1953 (this from a book by John
Littlewood, published that year):
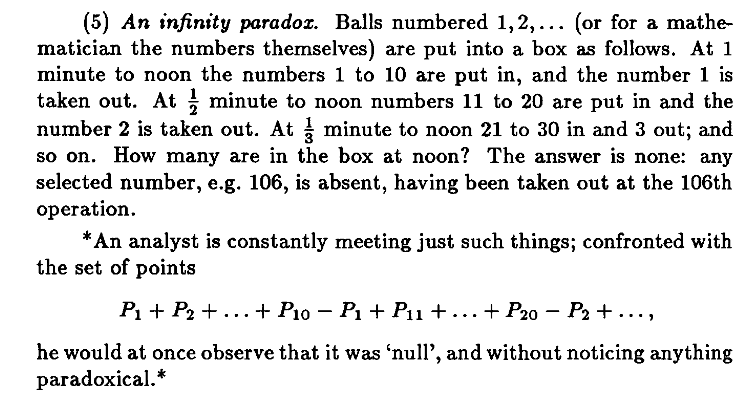
Just FYI, Littlewood has a lot of cred. He was the doctoral advisor of Srinivasa Ramanujan.
- We looked at two different scenarios: while continually dumping in
10 balls and taking out 1, we could
- Take the balls out in order, 1, 2, 3, 4, ....
What's a formula for when we would have pulled out the \(n^{th}\) ball?1
- Take the balls out by 10, 20, 30, 40, ....
What's a formula for when we would have pulled out the \(10*n\) ball?2
(exactly the same!)
That's what makes this paradoxical.
- Take the balls out in order, 1, 2, 3, 4, ....
- Then we answered a few posers about sets (especially infinite sets).
Question of the day:
- Let me ask if there are any questions about infinity generally
before we get started. We've been doing a lot of strange stuff,
so it might be good just to check in -- especially with a quiz
coming up!:)
- Before we get to our next paradox, let's look at one more
variation of that thought experiment, the ping-pong ball
conundrum:
Imagine that we fill the barrel with the ping-pong balls first, and then take out the balls on the old schedule: \[ n \longrightarrow 1-\left(\frac{1}{2}\right)^n \]
How many balls will be left in the barrel at the end of the minute?
Does this feel different (perhaps better) than the first telling, in which we were dumping 10 balls in for every ball we took out?
- Here's a strange question, and I think that this is one of the
trippiest discoveries of the course:
What do you think: are there more more points on the square itself than there are on the edge of the square?
This is related to the Hilbert Hotel, only the rooms are given by real numbers between 0 and 1 (say, if we talk about the unit square, with edge length equal to 1).
This picture lays out the problem, as well as the solution:
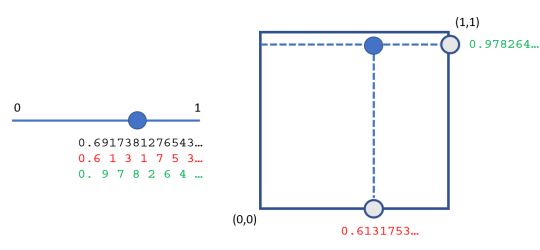
But the solution led to a lot of consternation all around:
"Certainly the two dimensional square must be a larger infinite set than the one dimensional line segment. Remarkably, Cantor showed that these two sets were the same cardinality. In his 1877 correspondence of this result to his friend and fellow mathematician, Richard Dedekind, even Cantor remarked, "Je le vois, mais je ne le crois pas!" ("I see it, but I don't believe it!" source)
This is an extension of the notion that even a countably infinite number of infinite school buses won't overwhelm Hilbert's Hotel; here even an uncountable number of copies of the line segment won't overwhelm the line segment....
- What do you think: are there more more points in a cube or on the
edge of the cube?
Upshot: there is a one-to-one correspondence between every point in this room and to a wee little line segment that we could draw on the board....
- Today we consider one final famous paradox, which we'll call "the
dartboard conundrum".
This paradox is about "the continuum" -- essentially the real numbers. The number of points covering the area of a dartboard is the same size as the infinite set of real numbers -- bigger than the natural numbers.
Start with a standard dartboard -- a circle -- and a standard dart (but very sharp).
The dart is so sharp that it hits just a single point in the dartboard's surface; you're such a good dart thrower that you hit the dart board every time. In other words, the probability is 1 that you will hit a point on the board. But otherwise you have terrible aim, so the probability that you'll hit any particular point on the dartboard is the same as it is for every other point.
(It's a thought experiment, okay?:)
Here's the question: Select any point on the dart board: what's the probability that you'll hit it?
Here's the paradox:
- If you assign it a positive probability, then, since every point has the same probability, you'll end up with a probability greater than 1.
- If you assign is a zero probability, then since every point has the same probability, you'll end up with a probability equal to 0.
- But, in the end, you hit a point!
Links:
- Ross-Littlewood
paradox (the older name of "the ping-pong ball conundrum")
Here was the earliest known reference to the conundrum:
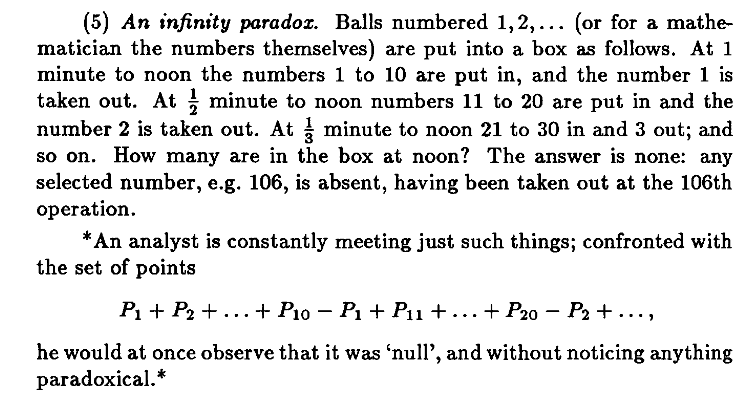
(from Littlewood's Miscellany)
- Was Cantor Surprised?