Day 29, Mat128: Calculus A

• Chain Rule Homework
• Chain Rule Worksheet

• Fun activities
• Free lunch! (Yes, there is!)
• Here's the link to sign up!

• $F(x)=4 + 0.35 \sin(2 \pi t / 5.4)$ What's the period and amplitude of \(F\)'s oscillation?
• Trickier: $F(x)=\sin(\sqrt{1 + x^2})$

  When you have a composition of three or more functions, I find the "stuff" method particularly useful, because it's recursive, and you only have to focus on one function at a time -- the "outside" function -- the final function in the "chain".

We'll approach this topic via four examples, making good use of the chain rule:

• Let's begin with the preview example, because it shows off some of the nice features -- and is a really important inverse function, to boot (because different nations use different systems, we frequently have to translate between these two systems -- at least I do, in Canada!).
  1. These inverse functions have a nice symmetry about the line $F=C$: they're reflections about the line $C=F$.
  2. If the point $(x,y)$ appears on one graph, then the point $(y,x)$ will appear on the other graph. (This just restates the first observation!)
  3. The slopes of the two lines are multiplicative inverses of each other.

  And that's pretty much the graphical version of the Preview!:)

• We now move on to a nice, friendly polynomial: $x^2$
  • Inverse functions undo the work of their function partners. Probably one of the first inverse functions you encountered in your mathematical career is the square root and its partner the square. We will denote the function and its inverse this way: if the square function is called $f$, then its inverse will be called $f^{-1}$:

    (WARNING: don't be fooled by the notation: $f^{-1}(x)$ is the inverse function; $f(x)^{-1}$is the multiplicative inverse, $\frac{1}{f(x)}$. They are completely different animals!)

    \[ f(x)=x^2 \] and \[ f^{-1}(x)=\sqrt{x} = x^{\frac{1}{2}} \]

    This is an interesting place to start, because the square function isn't actually invertible!

    By convention, we restrict the domain, and choose to consider the square function on only half of its domain (positive values of $x$).

  • Note that the portion of the square function to the right of the $y$-axis, and the square root function are just reflections of each other about the line $y=x$. This is always the case for inverse functions.

    And you can see what goes wrong if we try to reflect the part to the left of the $y$-axis: the inverse "function" would fail the vertical line test -- very naughty "function".

  • The important power of inverse functions is that they "undo" each other. This is expressed as follows: \[ f(f^{-1}(x)) = x \] and \[ f^{-1}(f(x)) = x \]

    It's unfortunate that we, being lazy mathematicians, will typically use \(x\) as the variable in both of these formulas. If we call \(g(x)=f^{-1}(x)\), and we think of \(x\) as belonging to the domain of \(g\), \(D_g\), then it would be better to write \(y=g(x)\), where \(y\) is in the range of g, \(R_g\), and then \(f\) takes things in the range of \(g\), and returns them to the domain of \(g\) (which lies in the range of \(f\), \(R_f\). A picture helps of course!

    

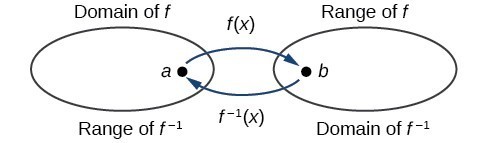
    Hence

    \[ f(g(x)) = x \] but \[ g(f(y)) = y \]

  • Now it's possible to figure out the derivative of the square root function without using the power rule for fractional powers.

    We simply assert that, if the two functions are equal, then their derivatives must be equal, as well:

    \[ \frac{d}{dx}\left(f(f^{-1}(x))\right) = \frac{d}{dx}(x) \] Then, using the chain rule on the left, "f'(stuff)(stuff)'=1": \[ f'(f^{-1}(x)) \frac{d}{dx}\left(f^{-1}(x)\right) = 1 \] So \[ \frac{d}{dx}\left(f^{-1}(x)\right) = \frac{1}{f'(f^{-1}(x))} \] Let's see what that produces in this case: for $f(x)=x^2$, $f'(x)=2x$, so \[ \frac{d}{dx}\left(f^{-1}(x)\right) = \frac{1}{2f^{-1}(x)} = \frac{1}{2\sqrt{x}} = \frac{1}{2}x^{-\frac{1}{2}} \]

• The most important example we want to consider today is the inverse function of $f(x)=e^x$: we'll call it $f^{-1}(x)=\ln(x)$.
  • We're going to proceed exactly as we did before, only this time we're in luck: the function $f(x)=e^x$ is, in fact, invertible -- no need to restrict a domain!

  • Now how about its derivative? For $f(x)=e^x$, $f'(x)=e^x$ -- easy!

    So \[ \frac{d}{dx}\left(f^{-1}(x)\right) = \frac{1}{f'(f^{-1}(x))} \] becomes \[ \frac{d}{dx}\left(\ln(x)\right) = \frac{1}{e^{\ln(x)}} = \frac{1}{x} = x^{-1} \] Amazing! This is the "missing power" -- we didn't know how to get this particular derivative using the power rule (It would have come from the power $x^0$ -- but that's a constant, so it's derivative is 0. This creates a mysterious connection between powers and the exponential function, and its inverse, the log.)

    Notice that it's our friend the hyperbola. Notice also that this function is odd -- it should be the derivative of an even function. We can extend the $\ln(x)$ function to the left, by considering $\ln(|x|)$:

  • By the way, this allows us to now clearly understand those derivatives of other exponential functions. Consider, for example, the function \[ g(x)=2^x \] Because we now have the inverse function of $e^x$, we can write \(2=e^{\ln(2)}\) -- more generally we need to remember that, as inverses, \(x=e^{\ln(x)}\) -- at least for positive values of \(x\). And, last I checked, 2 is positive: \[ g(x)=2^x=\left(e^{\ln(2)}\right)^x = e^{\ln(2)x} \] That might look a little scary, but $\ln(2)$ is just a number -- approximately 0.69. So we can now compute the derivative of $2^x$ easily, thinking of it as a composition -- and so using the chain rule: \[ g'(x)=\ln(2) e^{\ln(2)x}=\ln(2) 2^x = \ln(2) g(x) \] More generally, if $g(x)=b^x$, \[ g'(x)=\ln(b) e^{\ln(b)x}=\ln(b) b^x = \ln(b) g(x) \] And the choice of $b=e$ gives that amazing function that satisfies \[ g'(x)= \ln(e) g(x)= 1 \cdot g(x)= g(x) \]

• One more important example we want to consider: the inverse function of $f(x)=\sin(x)$: we'll call it $f^{-1}(x)=\arcsin(x)$.
  • Just as before, but once again we have to restrict the domain: sine is not invertible. We have a choice, but it seems like the best place to think of sine as invertible is on the interval $[-\frac{\pi}{2},\frac{\pi}{2}]$:

  • Now how about its derivative? For $f(x)=\sin(x)$, $f'(x)=\cos(x)$ -- still easy! But this time it will be a little more unpleasant to compute $f'(f^{-1}(x))$. There's a trick you know, however: we can rewrite cosine in terms of sine, using our most important trig identity: \[ \sin(x)^2+\cos(x)^2=1, \] so \[ \cos(x)=\pm\sqrt{1-\sin(x)^2}, \] Hence \[ \frac{d}{dx}\left(f^{-1}(x)\right) = \frac{1}{\pm\sqrt{1-\sin(\arcsin(x))^2}} \] becomes \[ \frac{d}{dx}\left(\arcsin(x)\right) = \frac{1}{\sqrt{1-x^2}} \] where you will notice that I chose the positive "branch". Why?

    Look at sine on this interval. If it is increasing everywhere, its inverse must be increasing everywhere: and what does that say about its derivative?

• Your turn!

  There are two other functions which deserve our attention. We call their inverses "arctan" and "arccos".

  Do exactly the same thing that we've just done in these three examples, but with two other important functions:

  1. $f(x)=\tan(x)$ -- use restricted domain $(-\frac{\pi}{2},\frac{\pi}{2})$
  2. $f(x)=\cos(x)$ -- use restricted domain $[0,\pi]$