- We'll have a quiz today, at the end of the hour. They're ten minutes long.
The quiz will be over section 1.5.
- Your 1.5 (written) assignment is due today. Please hand that to the center aisle.
- Today we'll
- wrap up section 1.6
- start section 1.8
- You have a new assignment -- some problems from the textbook,
which will be due next Thursday. You also have some assignments
on IMath.
- Please put your rectangles away.
- Limit laws:
- We start with two especially trivial special limits:
- Constant rule $(f(x)=c)$:
$\lim\limits_{x\to{a}}c=c$ Here the function $f(x)=1$ is plotted. As $x \to 0$, the $y$-values head to 1. Well, more to the point, they never vary from 1! Quite a boring function....
- Identity rule $(f(x)=x)$:
$\lim\limits_{x\to{a}}x=a$ Here the function $f(x)=x$ is plotted. As $x \to 0$, the $y$-values head to 0. And the closer $x$ gets to 0, the closer $y$ gets to 0. That's the way it's supposed to work! Also a rather boring function: so predictable!
What can we do with those? We need more horsepower....
- Constant rule $(f(x)=c)$:
- Sum law: "the limit of a sum is the sum of the limits"
So what is this limit:
$\lim\limits_{x\to{a}}(x+c)$ This sum (and many other operations) satisfy the same pattern:
"The limit of a STUFF is the STUFF of the limits." So, in particular,
"The limit of a sum is the sum of the limits." $\lim\limits_{x\to{a}}(x+c)=\lim\limits_{x\to{a}}x+\lim\limits_{x\to{a}}c=a+c$ - Difference law
- Product law
- Constant multiple law:
- Quotient law (slight caveat here -- no zero denominators)
Suppose that $\lim_{x \to a} f(x)$ and $\lim_{x \to a} g(x)$ exist. Then \[ \lim_{x \to a} [f(x)+g(x)] = \lim_{x \to a} f(x) + \lim_{x \to a} g(x) \] \[ \lim_{x \to a} [f(x)-g(x)] = \lim_{x \to a} f(x) - \lim_{x \to a} g(x) \] \[ \lim_{x \to a} [cf(x)] = c\lim_{x \to a} f(x) \] \[ \lim_{x \to a} [f(x)g(x)] = \lim_{x \to a} f(x) \lim_{x \to a} g(x) \] \[ \lim_{x \to a} \frac{f(x)}{g(x)} = \frac{\lim\limits_{x \to a} f(x)}{\lim\limits_{x \to a} g(x)} {\text{ if }} \lim_{x \to a} g(x) \ne 0 \]
- Power law
\[
\lim_{x \to a} [f(x)]^n = [\lim_{x \to a} f(x)]^n
\]
where $n$ is a positive integer (the limit of a power is the power of the
limit).
- Root law:
\[
\lim_{x \to a} \sqrt[n]{f(x)} = \sqrt[n]{\lim_{x \to a} f(x)}
\]
where $n$ is a positive integer. Again, we can ``pass the limit inside''.
Again, a caveat: why can't we compute
\[ \lim\limits_{x\to{0}}\sqrt{x} \]
Because the function isn't even defined as x approaches 0 from the left (square roots of negative numbers are imaginary). So we have only a one-sided limit, that \[ \lim\limits_{x\to{0^+}}\sqrt{x}=0 \] Of course we can say that \[ \lim\limits_{x\to{1}}\sqrt{x}=1 \] Limits exists everywhere else on the domain of the sqrt function. - Putting these laws together
- Now that we've got the sum and product and constant multiple rules, what can we deduce?
- "Affine" rule, for one:
\[ \lim\limits_{x\to{a}}(mx+b)=ma+b \] - Then we can proceed to deduce that all polynomials have limits, and
furthermore that
$\lim\limits_{x\rightarrow{a}}P(x)=P(a)$ This is the conclusion of Exercise #55, p. 71, which says that polynomials are continuous, which we'll consider more in section 1.8.
How do we know? Well an nth degree polynomial can be written as a sum of constants $c_i$ multiplying powers of $x$, $x^i$: \[ P(x)=\sum_{i=0}^n c_ix^i \] Then the limit of the sum is the sum of the limits: \[ \lim_{x\to a}P(x)=\lim_{x\to a}\sum_{i=0}^n c_ix^i =\sum_{i=0}^n \lim_{x\to a}(c_ix^i) \] and then we use the constant multiple rule and the power rules, and we're done: \[ \lim_{x\to a}P(x) =\sum_{i=0}^n c_i\lim_{x\to a}x^i =\sum_{i=0}^n c_ia^i = P(a) \]
Exercise #56 says it's also true for rational functions, for every element of their domain.
- Take a look at a couple of the examples in the text, examples 5
and 6 on page 66. These both illustrate the limiting
process applied to the most
important definition in calculus:
$f'(x)=\lim\limits_{h\rightarrow{0}}{\frac{f(x+h)-f(x)}{h}}$ In this case, both show examples of a slightly different version of this most important definition, the derivative at a point $x=a$:
$f'(a)=\lim\limits_{h\to 0}{\frac{f(a+h)-f(a)}{h}}$ - Other Laws
- The squeeze theorem
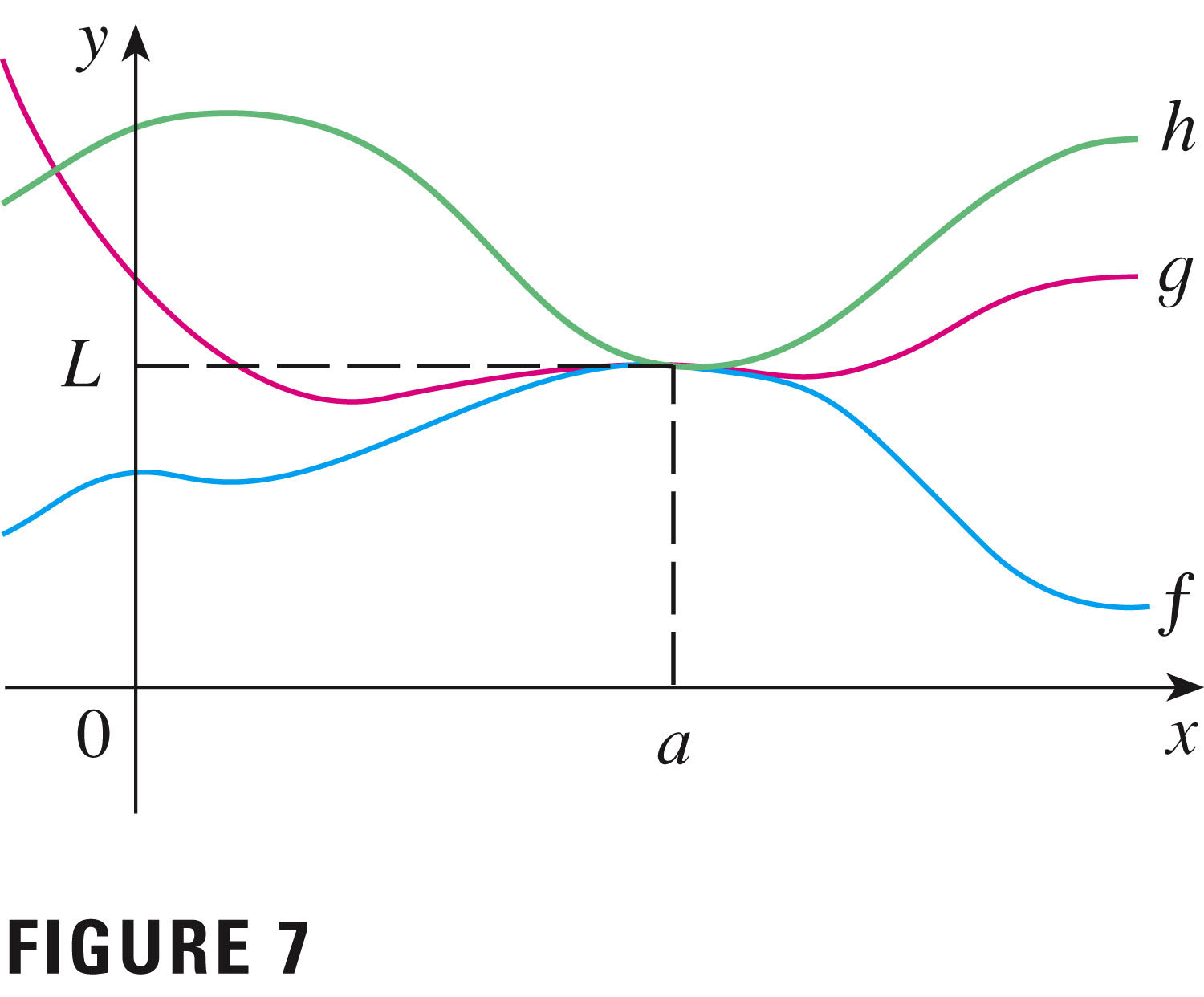
What's happening to the $y$-values?
- The squeeze theorem
- Now let's take a look at some of the examples from the section
exercises.
- Example 3, p. 65
- #7, p. 69
- #10 (see the theorem, p. 65)
- #25
- #33
- #47
- #63, p. 71
- #59, p. 71 (squeeze it!)
- We start with two especially trivial special limits:
- What is the difference between continuous and discontinuous things?
- A new administration in government?
- A sidewalk?
- Coffee poured into a cup?
- Definition: continuity at the point $x=a$:
\[
\lim_{x\rightarrow{a}}f(x)=f(a)
\]
Note: three things have to happen:
- The limit of $f$ exists at $a$,
- The function value $f(a)$ exists at $a$, and
- The two values are equal.
Otherwise $f$ is discontinuous at $a$.
There are various kinds of discontinuity (which we've already seen):
- Removable discontinuities (e.g. holes)
- Jump discontinuities
- Infinite discontinuities
- "Crazy discontinuities" like the function of #59, p. 71: $x^2$ for rational values of $x$, and 0 for irrational ones.
- Maybe a better definition:
A function is continuous on an interval if its graph can be traced there without lifting the pencil from the paper. (Try one! Make one smooth, and one really "jaggy".) Only one thing: Make sure that you're drawing a function! - Many of the functions we've considered so far satisfy this, although not all do: consider the "holy function"
\[
f(x)=\frac{\cos(x)-1}{x^2}
\]
This function has a limit at zero (-.5), but is not defined there. If $f$ is not defined at $x=0$, then it cannot be continuous there. We can fix this, by the way.... Just define $f(0)$ to be the limit (the closed dot in the graph above).
- Since continuity is wrapped up with limits, we have the same kinds
of results that we did in relation to limits:
- We define one-sided continuity
- we have sum laws, product, and quotient laws. We've already used these to demonstrate that polynomials are continuous on all real numbers: \[ \lim_{x\to{a}}P(x)=P(a) \]
- Classes of functions that are continuous on their domains:
- Polynomials
- Rational functions: (ratios of polynomials)
- Trigonometric functions: sine, cosine, tangent
- Root functions: $f(x)=x^{1/n}$
- Exponential functions: $f(x)=b^x$
- For all these functions one can evaluate limits using the
so-called "substitution method": simply plug in $a$ for
$x$.
- An important theorem (p. 88), RE composite functions (remember
that I told you how important compositions are? Here's another place
they show up....):
- Roughly: the composition of continuous functions is
continuous.
- Let $F(x)=f(g(x))$ be a composite function.
If $g$ is continous at $x=c$ and $f$ is continous at $g(c)$ then
$F(x)$ is continuous at $x=c$.
- Roughly: the composition of continuous functions is
continuous.
- Examples:
- pp. 90-93, #3, 10, 12, 19, 23, 36, 46 (with Mathematica)
- That crazy function which was $x^2$ for rational values of $x$, and 0 for irrational ones, has an interesting property: it is continuous at only a single point! It satisfies the definition only at $x=0$: it's discontinuous everywhere else! That's pretty weird.
- The Intermediate Value Theorem is an important result of continuity:
- Theorem: Suppose that f is continuous on the closed interval [a,b] and let N be any number between f(a) and f(b), where $f(a)\ne{f(b)}$. Then there exists a number $c$ in $(a,b)$ such that $f(c)=N$.
- Example: pp. 93, #69
- Theorem: Suppose that f is continuous on the closed interval [a,b] and let N be any number between f(a) and f(b), where $f(a)\ne{f(b)}$. Then there exists a number $c$ in $(a,b)$ such that $f(c)=N$.