- Your exams are returned:
- The exam.
- Statistics (before curve):
- Mean: 47
- Median: 49.5
- SD: 15
- The key (plus another take on Problem 5)
- The curve: add 3 to your score, then calculate the percentage.
- Some comments:
- There are a lot of positive things happening in the key (but they need to happen for everyone).
- I'm having some (but fewer than expected) problems with the limit definition. Good!
- There are still some severe algebra problems plaguing some of you. Here are some algebra magic tricks!
- Please consider using the Math/Stat Lab. Those who used it did better on this exam than those who have not. They send me records of who has used it!
- The exam.
- 2.3 homework was returned last time: graded the first two
problems.
- You have an assignment to hand in a week from now (section
2.4). You also have some IMath due Friday, so please keep an eye on
that.
- Please put your rectangles away.
- The derivatives of trig functions rely on some basic
understanding of the circle:
- Radian measure: there is a linear relationship between radians and degrees:
\[
Radians=\frac{2\pi}{360}Degrees
\]
In calculus, we almost always use radians. You should
try to start thinking in terms of radians, too.
- Length of a sector, related to angle $\theta$ subtending
and radius $r$:
Arc Length: $L = \theta r$
Again, this is an example of a linear relationship, but it's called "bi-linear", because it's linear in two different ways: $L$ is proportional to each of $\theta$ and $r$. So
- if you double the radius, you double the arc length;
- if you double the angle, you double the arc length.
Now you might wonder if there should be, or could be, an extra constant in there, but you can see that the formula works out for the circumference formula for a circle: \[ \theta=2\pi, \textrm{ so } L=2 \pi r \]
Yep! That's the formula for the circumference of a circle.
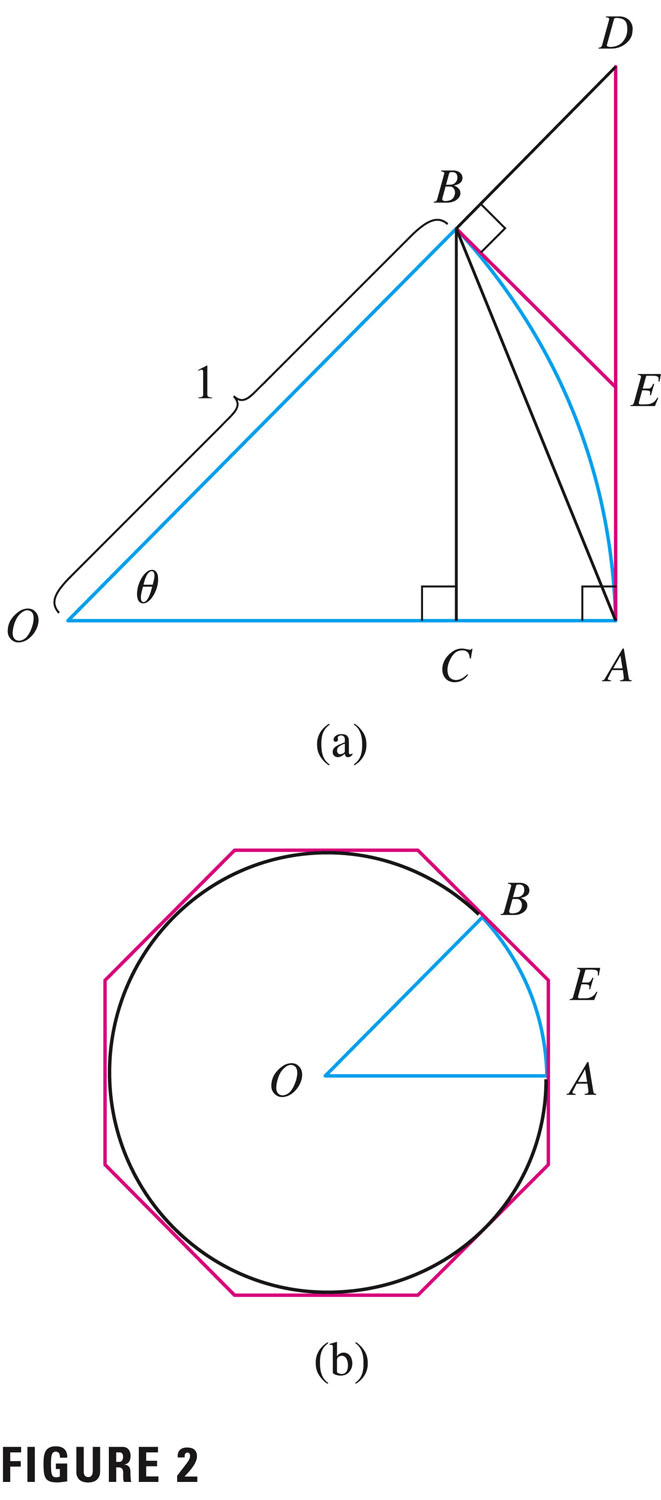
We can use this diagram (and the arc length formula) to prove a really important limit: \[ \lim\limits_{\theta \to 0}{\frac{\sin(\theta)}{\theta}}=1 \]
(See page 142, which I'll walk you through now. The proof uses some elementary trigonometry, plus the squeeze theorem, which is one of the really cool things about this proof!)
- Definitions of the trig functions, as functions of $x$, in radians (which is how we think about them in calculus):
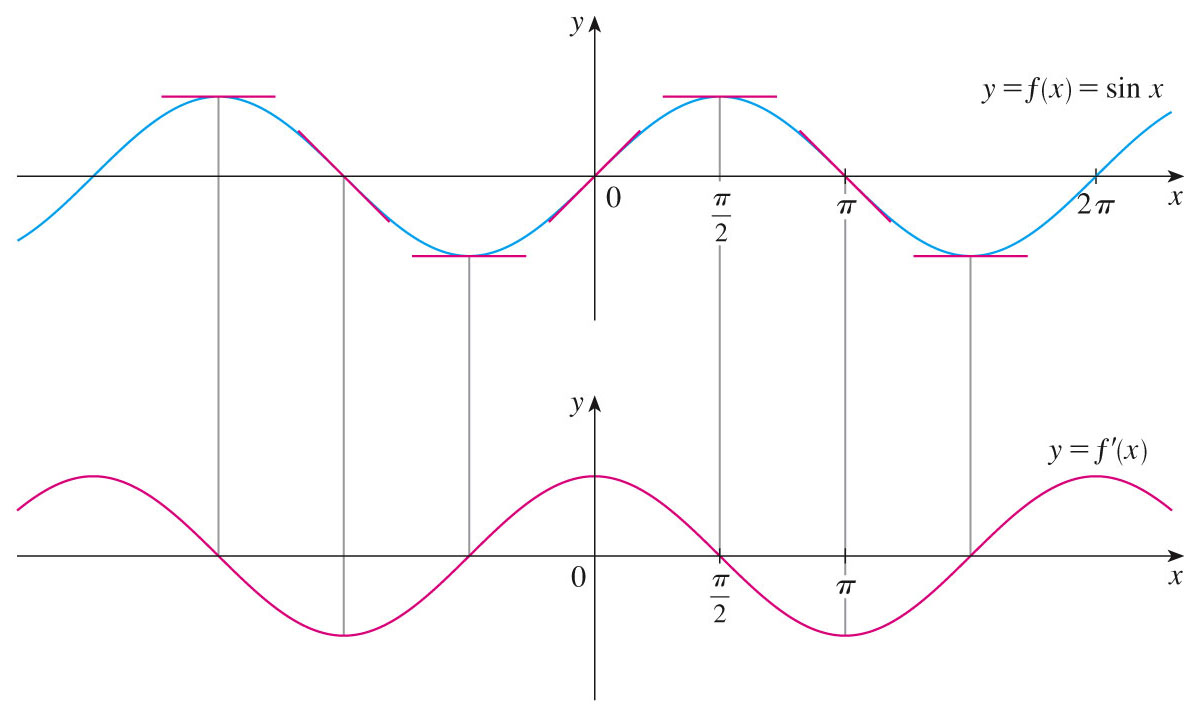
We will derive the derivative of the sine function from the limit definition of the derivative (although we can see the derivative graphically above).
There are exactly three important trig identities one needs to know (all the others can be derived from these three):
- The Pythagorean theorem:
$\sin^2(x)+\cos^2(x)=1$ - The sine of a sum:
$\sin(a+b)=\sin(a)\cos(b)+\sin(b)\cos(a)$ - The cosine of a sum:
$\cos(a+b)=\cos(a)\cos(b)-\sin(a)\sin(b)$
So let's see how to derive the derivative of the sine from the MIDIC -- the Most Important Definition In Calculus -- the limit definition of the derivative -- using the second of these identities, plus one more important limit (which can be proven with conjugates, and the first limit we derived): \[ \lim\limits_{\theta \to 0}{\frac{\cos(\theta)-1}{\theta}}=0 \]
Then the derivative of the cosine can be derived by simply shifting the sine function, and using the second trig identity above.
- Radian measure: there is a linear relationship between radians and degrees:
\[
Radians=\frac{2\pi}{360}Degrees
\]
In calculus, we almost always use radians. You should
try to start thinking in terms of radians, too.
- A few more applications of trig function derivatives, and then it's on to section 2.5: the chain rule.
- Derivative of tangent
- Fourth derivative of sine, cosine
- #7, p. 146
- #26
- #35
- #49 and 50
- The chain rule is so critically important because of the
importance of compositions of functions: for
$F(x) = f(g(x))$,
$F^\prime(x) = f^\prime(g(x))g^\prime(x)$ I personally think this to myself: "f prime of stuff times the derivative of the stuff"; or "f prime of stuff times stuff prime.",
where $f$ is the "outside" function:
$F^\prime(x) = f^\prime(stuff)stuff^\prime$ You can see that the rule is fairly simple, once you've identified the composition -- that is, once you've torn apart $F$ to find $f$ and $g$.
You might take a look at this summary from my pre-calc class to review compositions.
- The difficulty is often identifying the composition. We'll try
some easy ones first, then get to some ugly ones.
Before we do that, however, I'd like to show how to derive the chain rule, using the limit definition of the derivative. Everything comes from that! I'll need to use a result from p. 153, where the chain rule is proved in our text.
Basically, however, it relies on the tangent line: we want to use the fact that
$f(x+h) \approx f(x) + hf'(x)$ Why does that make sense? Because it comes straight out of the limit definition, where we throw away the limit. That's why we have to write "$\approx"$:
$f'(x) \approx \frac{f(x+h)-f(x)}{h}$ - #9, p. 154
- #16
- #29
- #42
- #77
- A Chain Rule tutorial
- A sample problem involving compositions: model the seasonal variation in Keeling's CO2 data:
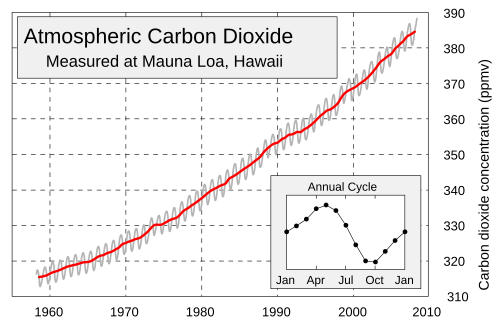
- Keeling data with models:
If time were measured in years from January, would
$V(t)=A\sin(2\pi{t})$ be a good model? What would be a good choice for the parameter $A$?