Day 48 in Mat229

1. Use composition; write out the series, to see what the terms look like.
2. Use parentheses: a bunch of you wrote \(2n+1\) when you meant \(2(n+1)\).
3. Both the AST and Taylor error estimate give the same thing! \(\frac{1}{120}\).
4. Did you notice that I gave you a few hints in the second and third problems to help you with the first?
5. The Key

I'm going to try to make Thursday's portion independent of calculators -- but we'll see. Bring one, just in case.

• A bit of a review: tangent lines require computing derivatives, of course. First derivatives of \(dy/dx\) will be computed using the chain rule:

  \[ \frac{dy}{dx} = \frac{dy}{dt}\frac{dt}{dx} = \frac{\frac{dy}{dt}}{\frac{dx}{dt}} \]

  If you read along in our text, you'll see that, from the motion perspective, we are often more concerned with \(dx/dt\) and \(dy/dt\). However, it is often of interest to find out where a particle is at a particular point along the "backbone curve" \(y=f(x)\), along which the motion proceeds.

  Let's think about uniform circular motion, for example, with \[ \begin{array}{c} {x(t)=\cos(t)}\cr {y(t)=\sin(t)} \end{array} \]

  1. Where does the motion begin (i.e. where are we when \(t=0\))?
  2. In what direction does the motion proceed?
  3. If we cut the string how will the object fly away?
  4. What is the slope of the tangent line anywhere (as a function of time)?
  5. So how can we write the tangent line at a given moment in time, \(T\)?

     We have a point: \((x(T),y(T))\); and we can calculate the slope, via \[ m(T) = \frac{dy}{dx} \bigg\rvert_{t=T} = \frac{\frac{dy}{dt}}{\frac{dx}{dt}} \bigg\rvert_{t=T} \]

     Then \[ y-y(T)=m(T)(x-x(T)) \]

• A note about the second derivatives of $y$ with respect to time (acceleration, or concavity).

  Suppose we also want to compute the second derivative, \[ \frac{d^2y}{dx^2} \]

  when faced with parametric equations $x=f(t)$ and $y=g(t)$.

  It turns out to be just another application of the chain rule. The first derivative gets us started:

  \[ \frac{dy}{dx} = \frac{\frac{dy}{dt}} {\frac{dx}{dt}} \equiv m(t) \] For the second derivative, we simply do it again -- but now we already know $\frac{dy}{dx}$ as a function of time (I called it $m(t)$ above), so \[ \frac{d^2y}{dx^2} = \frac{d}{dt} \left(\frac{dy}{dx}\right) \frac{dt}{dx} = \frac{\frac{d}{dt} \left(m(t)\right)} {\frac{dx}{dt}} = \frac{m'(t)} {\frac{dx}{dt}} \] It's a two-stage process. And obviously we could continue, computing third, fourth, etc. derivatives for the path in space.

• Note that finding the area under a parametric curve is also just an exercise in the application of the chain rule (Theorem 7.2 in the text): \[ A = \int_a^b y(x) dx = \int_{t_a}^{t_b} y(x(t)) \frac{dx}{dt} dt \] where \(x(t_a)=a\) and \(x(t_b)=b\)
• Materials:
  • Calculus of Parametric Equations (.nb)
  • Calculus of Parametric Equations (.pdf)

• We're just "changing coordinates" -- when one system makes more sense than another. If things are orbiting some center, say, then it makes more sense to use a polar coordinate system, like the one below, which shows how the angle \(\theta\) is measured:
  

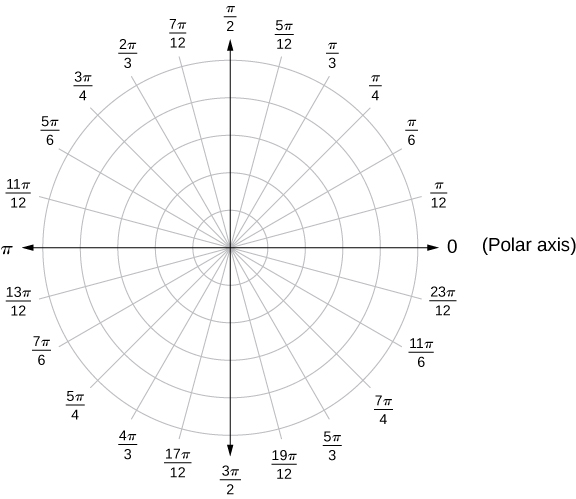
  If \(r\) is the distance of a point \((x,y)\) from the origin, then we can write that

  \[ x(r,\theta) = r\cos(\theta) \hspace{1in} y(r,\theta) = r\sin(\theta) \]

• Materials:
  • Polar Coordinates (.nb)
  • Polar Coordinates (.pdf)