Day 53 in Mat229

• Polar Coordinates (.nb)
• Polar Coordinates (.pdf)
• Polar plotting example from our handout

In particular, we want to talk about area of polar curves.

Let's start with a circle of radius r, centered at the origin, and see how we might adapt the "familiar formulas" to more exotic shapes:

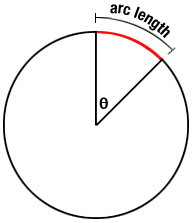
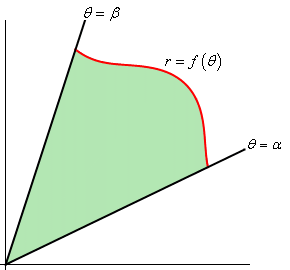
In the more exotic shape, and in contrast to the circle, the radius $r$ will vary as a function $f(\theta)$ as $\theta$ varies from $\alpha$ to $\beta$.

• Length: The arc length of a sector of the circle swept out by angle $\Delta \theta$ is given by $r \Delta \theta$ (with the familiar circumference formula being the case of sweeping out an angle of $2{\pi}$.

  If we let the angle \(\Delta \theta\) become infinitesimally small, the formula for arc length swept out is $rd{\theta}$. We integrate for a circle of fixed radius $r$ to get \[ L_{circle} = \int_{0}^{2\pi} r d\theta = 2\pi r \] (the circumference formula!), as we would expect. How must we adapt things if $r$ varies, as $r=f(\theta)$?

  This image from our text is enlightening:

  

  If you look at one little slice-of-pie-shaped section, you see that the arc length looks like the hypothenuse of a small triangle (and will look more and more like that as the size of the angle \(\Delta \theta\) shrinks to zero).

  So we need to tweak that arc length of a circle integral just a bit, to incorporate the change in \(r\) with \(\theta\): \[ L = \int_{a}^{b}{ \sqrt{ (r d \theta)^2 + dr^2 } } = \int_{a}^{b}{ \sqrt{ r^2 + \left( \frac{dr}{d\theta} \right)^2 } }\ d\theta = \int_{a}^{b}{ \sqrt{ f(\theta)^2 + f'(\theta)^2 } }\ d\theta \]

  Notice that this formula give the proper result in the case of a circle of radius $r$ centered at the origin, because in that case the second piece -- $\frac{dr}{d\theta}$ -- is 0! There is no change in $r$ as $\theta$ changes, so the rate of change is 0....

• Area:

  What is the area of a wedge from a circle of radius \(r\) subtended by an angle \(\Delta \theta\)? It's the fraction of the total area swept out by \(\Delta \theta\):

  \[ \Delta A = \pi r^2 \left(\frac{\Delta \theta}{2\pi}\right) = \frac{1}{2} r^2 \Delta \theta \]

  Alternatively, we can think of the area of a sector as basically that of a wedge, which is about half a rectangle (and this approximation gets better and better the smaller the value of $\theta$).

  Thus, in the picture above, \[ \Delta A \approx \frac{1}{2} (r)(r \Delta \theta) = \frac{1}{2} r^2 \Delta \theta \] (recall arc length above is approximately $r \Delta \theta$).

  Hence, when we have an infinitesimally small angle $d\theta$, the approximation should be exact: $dA=\frac{1}{2}r^2d\theta$, and \[ A=\int_{\alpha}^{\beta} \frac{1}{2}r^2\ d\theta =\frac{1}{2} \int_{\alpha}^{\beta} f(\theta)^2 \ d\theta \] is indeed the area of that shaded region on the right above.

• Calculus of Polar Equations (.nb)
• Calculus of Polar Equations (.pdf)