- Your quizzes are returned.
- There's a homework due today, and I've pushed our 14.4 homework back, due next Tuesday.
- Before we begin, any questions about things?
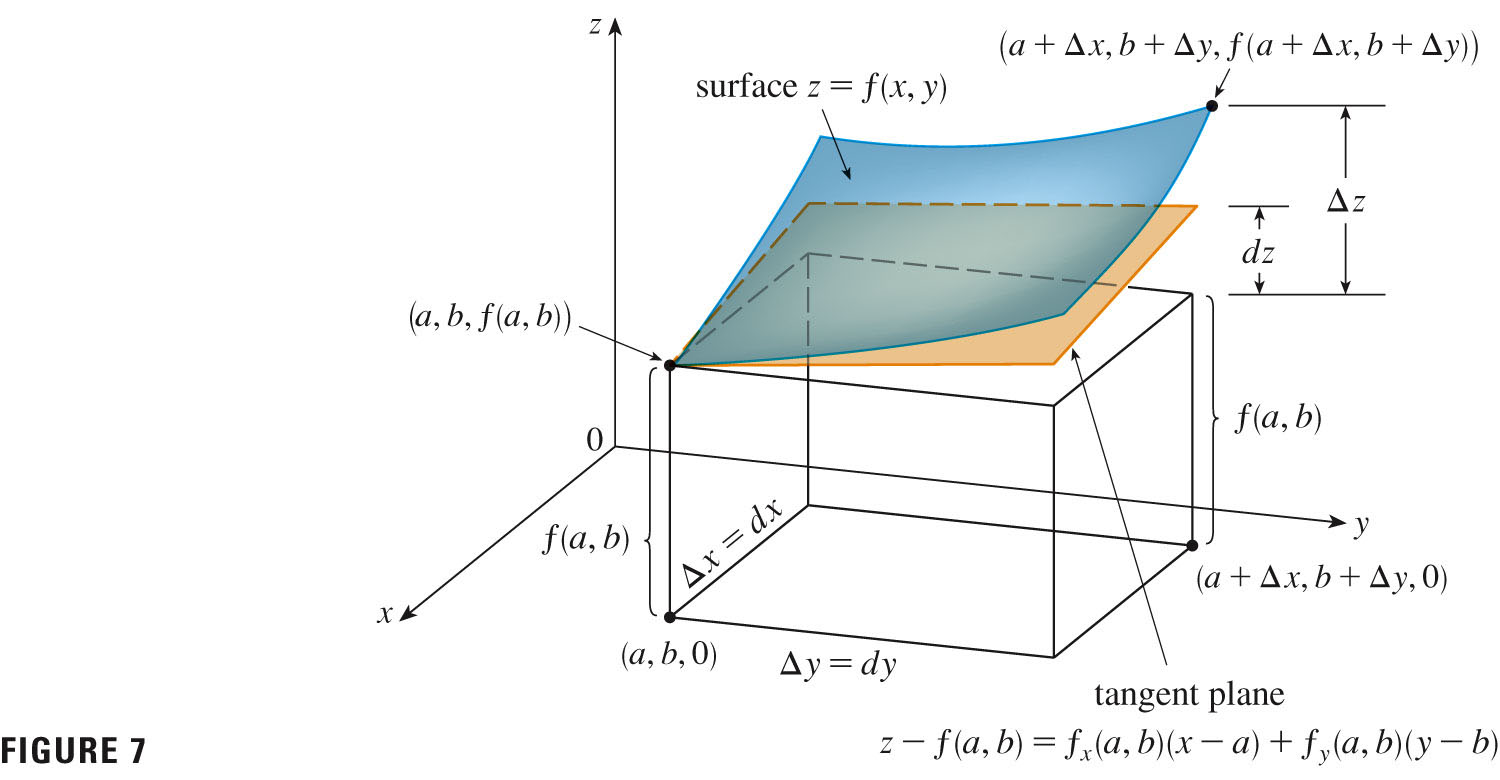
Just like univariate derivatives are closely linked to tangent lines, which kiss a curve (osculate); about the slopes of those linear approximations (tangent lines) to a univariate function; so are partial derivatives are about slopes of univariate functions obtained by slicing multivariate functions with planes. If the function is differentiable at a point, then there is a tangent plane, which kisses the surface.
An example from our author's TEC animations.
- Here's a Mathematica
file for similar problems which I stole from someone at the Air Force Academy....
- The tangent plane, provided it exists, is given by three points on
the surface (provided they're not co-linear). You can find three points
using the point at $(a,b)$, and points obtained by moving along the
cross-sections in the $x$ and $y$ directions.
The slopes in those directions are given by $f_x(a,b)$ and $f_y(a,b)$ as you set off from point the $(a,b)$.
If you take a one-unit step in either of those directions, the $z$-value would rise by either slope: \[ T(x,y)=f(a,b)+f_x(a,b)(x-a)+f_y(a,b)(y-b) \] If you take partial derivatives of $T$ at $(a,b)$, you will see that the partials (and the function value) agree with those of $f$ there.
- Strange things can happen, such as Example 4, p. 941. Let's take a look at
that one.
- #46, p. 944
- Use the limit definition to show existence
- Use two different approaches to show failure of continuity (limit doesn't exist)
- To finish this up, we turn to #45.
- #45: differentiability implies continuity; hence, if the function
of #46 is not continuous at (0,0), then it is not differentiable at (0,0).
- So, to wrap up #46, we show that the partials are not continuous at (0,0) (fail to have limits). If not, the function of #46 would be differentiable, and the linearization would be a tangent plane for the function. As it is, this function has no tangent plane at the origin.
To prevent problems, we introduce the following definition:
If $z=f(x,y)$, then $f$ is differentiable at $(a,b)$ if the increment $\Delta z$, which is the actual change in function values between the two points \[ \Delta z = f(a+\Delta x,b+\Delta y) - f(a,b) \] can be expressed in functional form as \[ \Delta z = f_x(a,b)(x-a) + f_y(a,b)(y-a) + \epsilon_1 \Delta x + \epsilon_2 \Delta y \] or \[ \Delta z = f_x(a,b)\Delta x + f_y(a,b)\Delta y + \epsilon_1 \Delta x + \epsilon_2 \Delta y \] where $\epsilon_1$ and $\epsilon_2 \to 0$ as $(\Delta x, \Delta y) \to (0,0)$.
We can generally avoid using this definition, however, because of Theorem 8, p. 942:
Existence and continuity of partials $f_x$ and $f_y$ are sufficient to imply differentiability.
That is, we can just check partials in two directions (but we require continuity of the partials for the function to be differentiable).
For a function $z=f(x,y)$, we define the differentials $dx$ and $dy$ to be independent variables; that is, they can be given any values. Then the differential $dz$, the total differential, is defined by \[ dz=f_x(x,y)dx + f_y(x,y)dy \] Differentials give us approximate changes to a function in the neighborhood of a point, generally when $dx$ and $dy$ are small, obtained by following along the tangent plane.
$\Delta{z}$ gives the actual change, so \[ \Delta{z}\approx dz=f_x(x,y)dx + f_y(x,y)dy \] The picture at the end of the section summarizes the situation nicely:
- #46, p. 944
- Let's take a look at the Discovery Project on p. 980, parts 1-3. This is
the natural extension of the tangent plane -- the tangent bowl.
- Why don't you carry out any analysis with a partner or two, and then we can check results with
- Some Mathematica code