Day 14 in Mat329

Last time

Next time

Today:

Announcements
- Your homework didn't get graded yet. I'm working on a grant application -- due at 4:30 today. Sorry about that. I'll hope to have them back by tomorrow.
- Check out my dad's viewmasters....
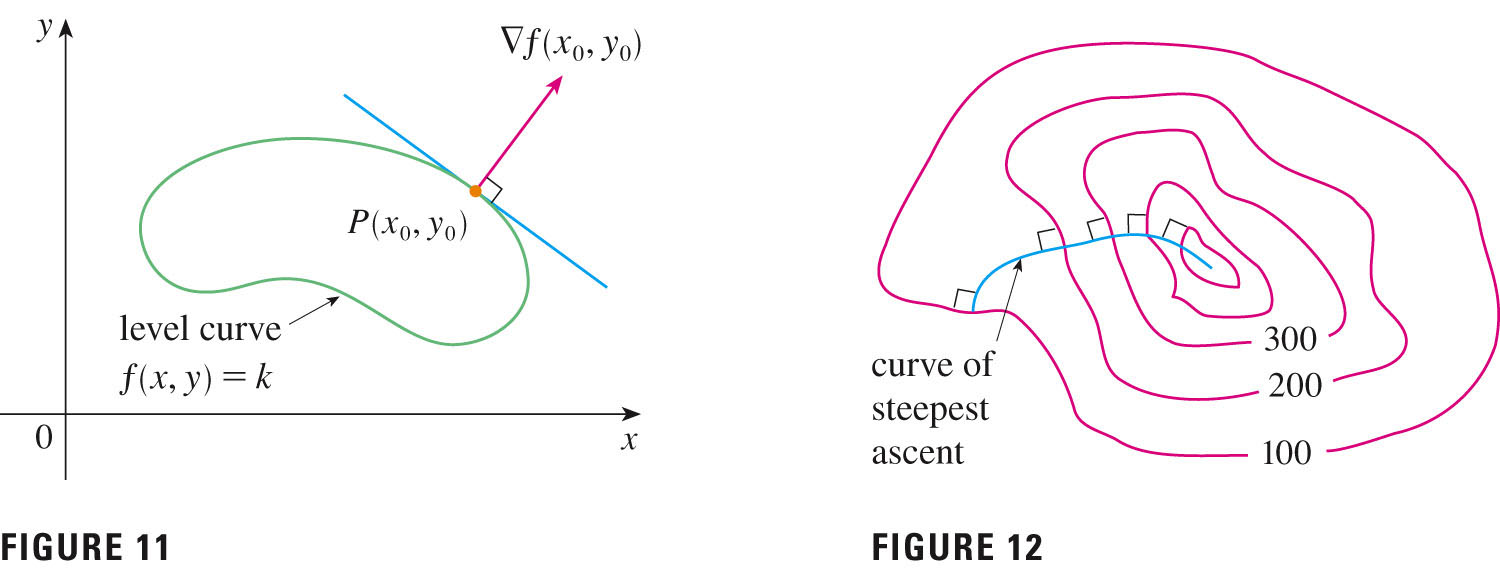
Last time we started section 14.6: the directional derivative and the gradient
We shouldn't be a stick in the mud about the orientation of our axes: why $x$ and $y$, and not some other pair of directions which are mutually perpendicular? Perhaps we are interested in the slope of the surface along some direction other than $x$ or $y$: hence the idea behind directional derivatives. At a given point at which a function is differentiable, one natural choice for two directions might be the direction in which the function is increasing fastest, and the direction perpendicular to this.
But any direction will do -- take a look at p. 957, Figure 3.

Our author's pretty good TEC animation of that figure.
This figure is partially what motivated me to create that "slicing" demo in Mathematica.
One of the biggest pieces of news is that we're going to be working with vectors -- e.g. $u$ -- and with vector-valued functions; and that will place another demand upon your visualization skills.
But gradients are just another kind of multivariate function: one where the domain is points in the plane, like many of our other functions, but the range is the set of vectors.
At each point in the plane there is a gradient vector pointing -- indicating what?
Are you comfortable with
- the two properties of a vector?
- unit vectors?
- dot products?
- norms?
Let's see each of these concepts "in action", to make sure that we're all on board with their definitions, and these other important definitions:
1. The directional derivative of $f$ at $(x_0,y_0)$ in the direction of unit vector ${\bf{u}} = \langle a,b \rangle$ is \[ D_{\bf{u}} f(x_0,y_0) = \lim_{h \to 0}\frac{f(x_0+ha,y_0+hb)-f(x_0,y_0)}{h} \] if this limit exists.
2. If $f$ is a function of two variables $x$ and $y$, then the gradient of $f$ is the vector function $\nabla f$ defined by \[ \nabla f(x,y) = \langle f_x(x,y), f_y(x,y) \rangle = \frac{\partial f}{\partial x} \hat{i} + \frac{\partial f}{\partial y} \hat{j} \]
3. Theorem: \[ D_{\bf{u}} f(x,y) = \nabla f(x,y) \cdot {\bf{u}} \]
4. More generally (in higher dimensions), we can write \[ D_{\bf{u}} f({\bf{x}}_0) = \lim_{h \to 0}\frac{f({\bf{x}}_0+h{\bf{u}} )-f({\bf{x}}_0)}{h} \] where $\bf{u}$ is a unit vector. (Isn't that a beautiful analogy with the limit definition of the univariate derivative -- the most important definition in calculus?)
5. Theorem: Suppose $f$ is a differentiable multivariate function. The maximum value of the directional derivative $D_{\bf{u}}f({\bf{x}})$ is $|\nabla f({\bf{x}})|$ and it occurs when ${\bf{u}}$ has the same direction as the gradient vector $\nabla f({\bf{x}})$.
Let's check out p. 966: significance of the gradient vector, then on to some examples from the exercises:
1. #1, p. 967
2. #5
3. #7
4. #22
Today we begin section 14.7: maximum and minimum values.
Consider the following problem: find all the local maxima and minima (and saddle points) of the function $f(x,y)=x^2+y^2+x^2y+4$.
As a polynomial, this has degree 3 (since we have an $x^2y$ term). This means that it is not restricted to the bowl or hyperbolic paraboloid of quadratic functions, but may have more interesting features. On the other hand, we should realize that, provided the function is twice differentiable at any point, it can be approximated by a "tangent bowl" there.
I've used the term "tangent bowl", but it could just as well be a "tangent saddle" (because that's another shape that a quadratic function of two variables can have).
So we expect the local behavior to have one of these two shapes (if we go beyond the tangent plane, to the tangent bowl/saddle/quadratic shape).
So how are we to determine the shape of $f(x,y)$, and discover the location of its extrema? The extrema at differentiable points will look like bowls or saddles, locally and generically.
There are other possibilities, however: for example, one can get troughs.
These were summarized well in that short note that my dad published in the American Mathematical Monthly, long, long ago, which I tried to recreate using Mathematica.
The main point is that "generically" (that is, almost all of the time) we have either a bowl or a saddle.
The univariate case is handled by considering the places where the derivative is equal to 0, and a very similar situation arises in the multivariate case: the analogy is that the gradient will equal the 0 vector.
The argument is simple, given on p. 970 (Theorem 2): let's go over it. Once again we rely on our understanding of univariate functions to arrive at this conclusion.

For the function $f(x,y)$ given above, we will find that there were two saddles, and a minimum. The graph of $f$ suggests it.
Now, how do we know that these are the only critical points, their locations, etc.? We compute the gradient vector, and set it equal to zero. This gives us a pair of equations to solve simultaneously for the critical points:
- $f_x(x,y)=2x+2xy$
- $f_y(x,y)=2y+x^2$
Setting these to zero simultaneously yields the three solutions
1. $(x,y)=(0,0)$
2. $(x,y)=(\sqrt{2},-1)$
3. $(x,y)=(-\sqrt{2},-1)$
Now how can we determine whether we have a minimum or a maximum or a saddle at a given critical point? If the second partials are continuous on a disk with center $(a,b)$, a critical point, then define \[ D = D(a,b) = f_{xx}(a,b) f_{yy}(a,b) - [f_{xy}(a,b)]^2. \] There are three cases:
1. If $D>0$ and $f_{xx}(a,b)>0$, then $f(a,b)$ is a local minimum.
2. If $D>0$ and $f_{xx}(a,b)<0$, then $f(a,b)$ is a local maximum.
3. If $D<0$, then $f(a,b)$ is neither a local maximum nor minimum (in this case, $(a,b)$ is called a saddle point.
So now we compute $D$:
- $f_{xx}(x,y)=2+2y$
- $f_{xy}(x,y)=2x$
- $f_{yx}(x,y)=2x$ (ah ha! we should have known better: this is a polynomial, after all....)
- $f_{yy}(x,y)=2$
Hence $D=4(1+y)-4x^2$. In two cases, $D$ is negative, and we have a saddle; in the other case, at the origin, $D=4$ and $f_{xx}=2>0$, so we have a local minimum.
If we're interested in absolute extrema, then we need to consider the boundary of a region, as well. There is an extreme value theorem for multivariate functions -- a natural extension of the EVT for univariate functions (p. 975).
Now let's take a look at some examples. I want to start with one of the most important, however: #55, p. 979, which illustrates the importance of a standard problem in the linear algebra.
- #3, p. 977
- #14, p. 978
- #32
- #50, p. 979
- #52

Website maintained by Andy Long. Comments appreciated.