- We're nearing the end! This is week 15.
Today we continue with polar equations for Lab 15.
- Zoom:
- Start it.
- Video on.
- Can everyone hear?
- Share screen.
- Record.
- I hope that your exam went well. I've not looked at them yet. I'm
in a bit of a backlog, but should be able to dig out
soon (no more tests in any of my courses -- hopefully
you can say the same!).
- So it's on to lengths and areas in Polar coordinates (pdf summary)
In particular, we want to talk about area of polar curves.
Let's start with a circle of radius r, centered at the origin, and see how we might adapt the "familiar formulas" to more exotic shapes:
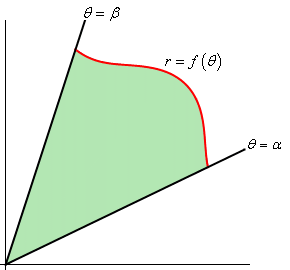
So as $\theta$ varies from $a$ to $b$, the radius $r$ will vary as $f(\theta)$.
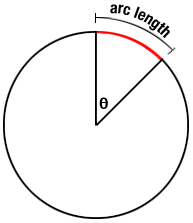
- Length: The arc length of a sector of the circle swept out
by angle $\theta$ is given by $r\theta$ (with the familiar
circumference formula being the case of sweeping out an angle
of $2{\pi}$.
In the case of a circle, the formula for length swept out is $rd{\theta}$. If we integrate for a circle of fixed radius $r$, we get \[ L = \int_{0}^{2\pi} r d\theta = 2\pi r \] (the circumference formula!). How must we adapt things if $r$ varies as $r=f(\theta)$?
It turns out that we need to tweak that formula just a bit: \[ L = \int_{a}^{b}{ \sqrt{ r^2 + \left( \frac{dr}{d\theta} \right)^2 } }\ d\theta = \int_{a}^{b}{ \sqrt{ f(\theta)^2 + f'(\theta)^2 } }\ d\theta \]
Notice that this formula give the proper result in the case of a circle of radius $r$ centered at the origin, because in that case the second piece -- $\frac{dr}{d\theta}$ -- is 0! There is no change in $r$ as $\theta$ changes, so the rate of change is 0....
From this we see that going from the specific to the general can be dangerous. That being said, we often do dangerous things, and sometimes they work. See what happens in the case of area!:)
- Area: For the circle, the area of a sector is basically that of
a wedge, which we can think of as about half a rectangle (and this
approximation gets better and better the smaller the value of $\theta$).
Thus, in the picture above, $\Delta A \approx r \frac{r \theta}{2}$ (recall arc length above is about $r \theta$).
Hence, when we have an infinitesimally small angle $d\theta$, the approximation should be exact: $dA=\frac{r^2}{2}d\theta$, and \[ A=\int_{a}^{b} \frac{1}{2}r^2\ d\theta=\int_{a}^{b} \frac{1}{2}f(\theta)^2 \ d\theta \] is indeed the area of that shaded region on the right above.
- Length: The arc length of a sector of the circle swept out
by angle $\theta$ is given by $r\theta$ (with the familiar
circumference formula being the case of sweeping out an angle
of $2{\pi}$.
- Materials:
- Equation of the cardiod: $r(\theta)=1-\cos(\theta)$
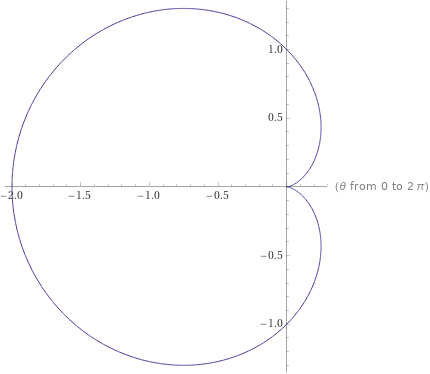
- Area of the cardiod: $A=\frac{1}{2}\int_{0}^{2\pi}(1-\cos(\theta))^2\ d\theta = \frac{3\pi}{2}\approx 4.71$
- Length of the cardiod: $L=\int_{0}^{2\pi}\sqrt{(1-\cos(\theta))^2+(\sin(\theta))^2}\ d\theta = 8$