Day 17, Mat128: Calculus A

I'll summarize before we move on to 1.8.

• There are some interesting ways in which functions can fail to have limits:
  

• Continuity/Discontinuity:
  

  Definition 1.7.6

• Summary:
  • Differentiability implies continuity (smoothness implies connectedness)
  • But continuity does not imply differentiability (connectedness does not imply smoothness); an example is a corner in a graph.
  • If \(f\) is differentiable at a point, it is locally linear there (is well represented by its tangent line), which leads us into our next topic: the local linearization!
  

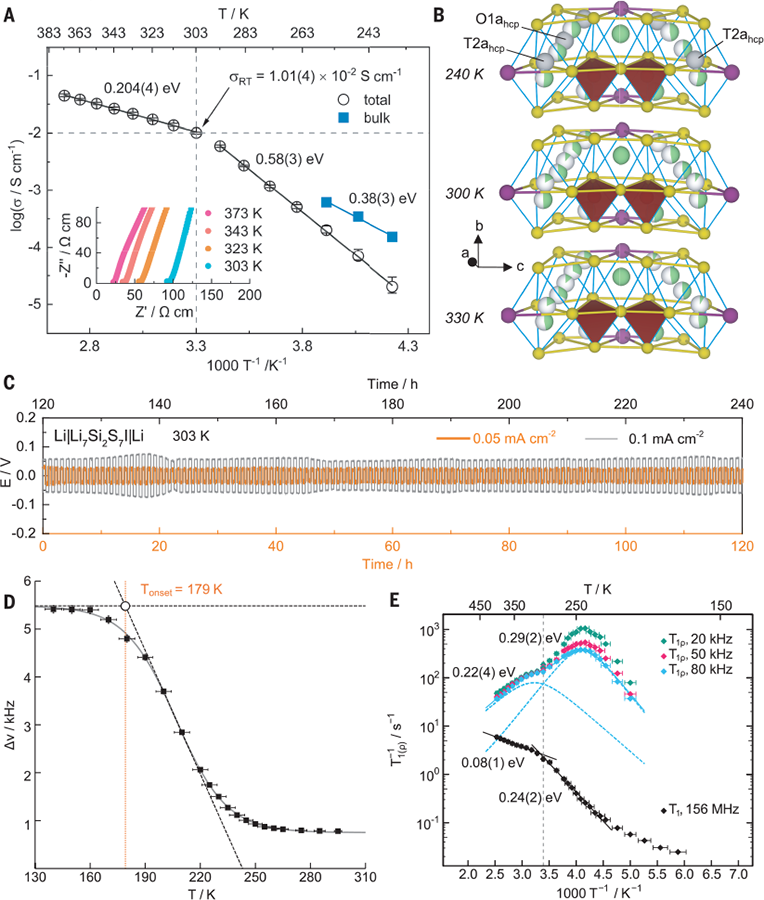
It illustrates various aspects of our course so far, including an important inflection point, concavity, the use of the tangent line, and also shows how well a tangent line can approximate a function over quite a wide interval. The function is "locally linear", and "locally' extends pretty far....

In a way this is also a bit of a review. That's the good news!

The upshot is that linear functions are good approximations to smooth functions (functions with derivatives), if you zoom in close enough.

• An important first step was using what we call the "linearization", the tangent line: we use the fact that \[ f(x) \approx f(a) + (x-a)f'(a) \] The right hand side we recognize as the equation of the tangent line.

  This comes straight out of the "alternative" limit definition, where we throw away the limit. That's why we have to write $``\approx"$: \[ f'(a) = \lim_{x \to a} \frac{f(x)-f(a)}{x-a} \approx \frac{f(x)-f(a)}{x-a} \]

  Solving for \(f(x)\), we obtain

  \[ f(x) \approx f(a) + (x-a)f'(a) \]

• The tangent line serves as an impressive approximating machine, provided $h=x-a$ is small enough. (How small is "small enough?")

  We can see why this works well if we get "small enough", if we visit the website suggested by our authors.

• That linear function given by the tangent line, $y = f(a) + f'(a)(x-a)$, is called the local linearization of $f$ at the point $(a,f(a))$:
  $L(x)=f'(a)(x-a)+f(a)$
  • For example, suppose you need to compute $\sqrt{15.96}$. Now the easy way is to use your calculator, but the cowboy way would be to use the linearization! Let's have a go at that one.
    • We know the square root of 16, which is close: our answer should be near 4. We choose a nearby value that simplifies our expression....

    • This picture demonstrates two slightly different types of quantities that we want to distinguish: differentials $dy$, and increments $\Delta y$.
      
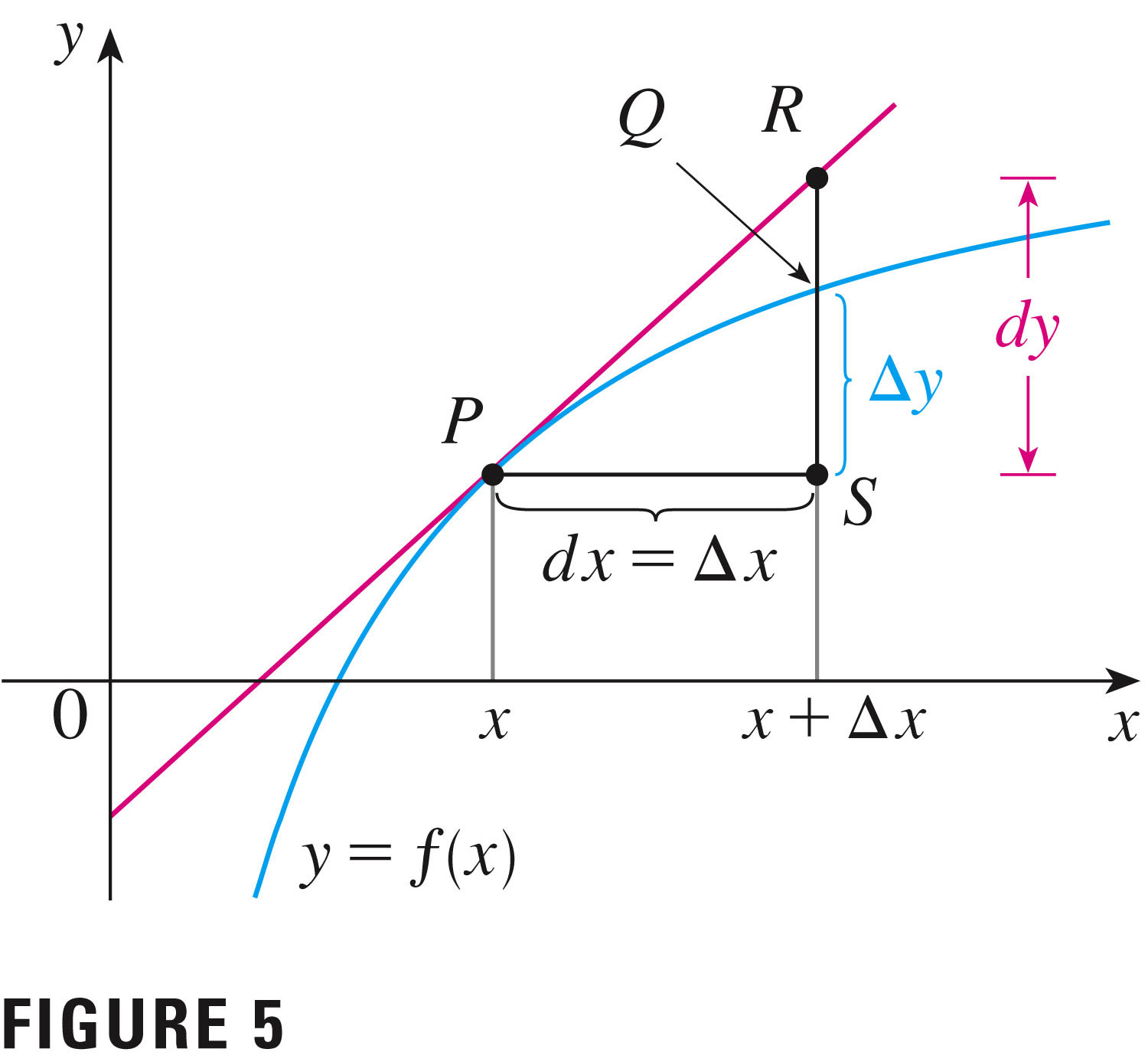
      • The increment $\Delta y$ is the true change in the function value;
      • the differential $dy$ approximates the true change.
      One way to remember the difference:
      • Differentials $dy$ follow the tangent line -- move in the direction suggested by the derivative
      • Increments $\Delta y$ follow the function -- are actual changes in the function value.

      $dy \approx \Delta y$

      We want the increment, but may settle for the easily computed differential.

    • So back to our example: compute the derivative of $f(x)=\sqrt{x}$ at $x=16$: \[ f'(x)=\frac{1}{2\sqrt{x}} \] so \(f'(16)=\frac{1}{8}\), and we can write down the tangent line equation: \[ L(x) = \frac{1}{8}(x-16) + 4 \]
      • What's the approximate value?
      • What's the actual value?

    • We use the tangent line for our approximation, and, when we're done, we can ask "is our answer an over- or an under-estimate?"

      The answer takes us back to the second derivative:

      

  • Let's have a look at today's worksheet (you'll be excited to know that there are more potato problems!:): we'll try some activities and homework problems from section 1.8.
    • Leftover Potatoes