Derivation of the Kriging Equations

We make the assumption that there is a ``Regionalized variable'' Z defined at each point on a region, for which we have N data locations ( ), and a value at each location . We are going to derive the best linear unbiased estimator (BLUE) of z, which we call , at a location x.

In the process of doing so, we will discover the necessity of making certain assumptions (known as the ``intrinsic hypothesis'') on the phenomenon under consideration in order for all to proceed nicely. Note that the weights multiplying the are actually functions of both x and .

Our strategy (expressed in mathematical terms) is as follows:

 

is a linear estimate of the ; we want to determine the such that

is a minimum, and such that the estimator is unbiased:

For the latter condition, we introduce the assumption that

for all locations x and y, in which case a sufficient condition for unbiasedness becomes

(Why is that 4?) Since we are considering only one location x, we have suppressed the dependence of on x and . You should remember that there is dependence, however, because the weights are not fixed, but must be recalculated at each location. I'll also use where I should really be using ; again, it just keeps things simpler.

One thus proceeds via constrained optimization (we constrain the weights to sum to 1). Taking advantage of this constraint, note first of all that

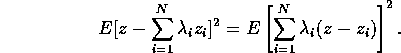
(Why is that 4?) The goal is now to minimize the function

 

where z=z(x) is the true value at the location x. Expanding the first term we find that

 

Note now that

(why is that 4?) and if we replace by this expansion in the sum (3), then we can simplify a little:

 

(Why is that 4?).

Differentiating with respect to (for each ) and leads to the following linear system of equations:

 

Without further assumptions we're stuck: we don't know what to do with the expectation; so let's make the assumption that the quantities and can be obtained from a model, which we will call the theoretical variogram. We make the assumption that

exists and is independent of location ( is simply a function of the difference of the locations). This is sometimes written

where we have indicated a vector quantity (e.g. ) by underlining it.

The two assumptions we made (the one above, plus the earlier assumption that the mean is constant) together comprise the so-called intrinsic hypothesis, which must be satisfied in order to derive the ordinary kriging equations.

Putting it all together, this system can be written in the matrix form

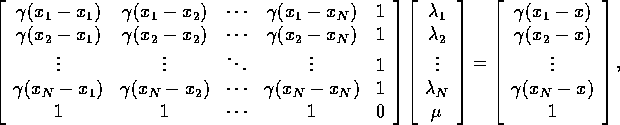
or more concisely as

 

where is the matrix of variograms ( ), is a column vector of 1's, and is a vector of variogram values relating the position at which one wishes the estimate (x) to the data locations ( ): .

Note the key role that the variogram function plays in this system of equations. We emphasize that the variogram is a function only of the difference in the positions of the two locations considered: this means that the theoretical variogram is the same over the entire study area.

Computations/Observations

The painful sides of kriging are as follows:

• The weights must be calculated at each location x.
• Although we would generally like to solve the system (6) with all data included, in general N is large, which means that the matrix system (6) is quite large. Solving such large matrix systems can be extremely slow, and solutions generally becomes more unstable as N gets large.

  The solution usually chosen is to restrict the number of points used to those which are closest to the estimation location. We know how to define closest: in terms of the range of the variogram. Any points beyond the range of the variogram are usually excluded. It may be necessary to limit the number of points anyway, as there may be many inside the range; so we select at most n, say, of the nearest neighbors.

• The weights are calculated by solving a linear system, which is (n+1) by (n+1) (where n is the number of neighbors used in the scheme). All the problems of solving linear systems thus become operative:
  • poorly conditioned matrices make for bad results; it could get so bad that
  • the matrix may be numerically singular (non-invertible), and hence we can not solve for the weights.

Kriging is touted as an interpolator (which means that the kriging surface passes through the data values at the data locations); but there is one issue that I believe is critical to understand:

if the model contains a nugget term, then the kriging surface will be a ``jump'' interpolator: that is, the surface will not tend toward the value as you tend toward the position , but rather leap up to meet .

The most obvious example of this is when you use only a nugget model. The kriging estimate is the mean away from the data locations, while at the data location the estimate is .

The upshot is that kriging does not always produce a smooth surface; one can say, however, that it will always be smooth except possibly at the data locations.

Now we turn to the essential issue of how to model the variogram.