- Your exams are returned. Covered sections were:
- 7.2 - trig integrals
- 7.7 - approximate integration
- 7.8 - improper integrals
- 8.1 - arc length
- 10.1 - parametric equations
- 10.2 - calculus with parametric curves
- 10.3 - polar coordinates
- 10.4 - area and arc length of polar curves
- 11.1 - sequences
- Exam 2
- Scores were low, as were spirits. To pick up both, we'll play one
of my favorite games: "Make up the test!" In this game, the
participants redo the exam, but do it perfectly right -- and then I
average the two scores. Hence if you have a 50% on your test now, and
do it perfectly this next time, you'll end up with a 75%. Much
better. You can get a copy from the link above, and you have one week.
I'll start by rounding anything below a 50% to a 50%, so the worst you should do -- if you do the repeat exam perfectly, which you should! -- is a 75%.
If you did a problem (or section of a problem) perfectly the first time, there's no need to repeat it. Submit both the perfect test, and your original test.
To make this even easier, here are some good tries, if not outright successes
- Now, unfortunately, for some negatives:
- My god, the dx-droppers outnumber those who don't!
I mention things directly in class, hoping that you'll all take the hint; but then you don't. For example, I mentioned that the integral improper of both types I and II, with "the obvious side" convergent (but the other divergent), would make a good test question. So there it is, Problem 1.a. We also talked about comparison during the review, so I put an "easy" one on there. But you all made it tremendously hard.
Since it's divergent on one side, the integral itself is divergent (and you're done). No need to consider the other type. Don't make more work for yourself -- you have enough to do.
There's a lot of "abstract nonsense". For example, integrating a positive function in the positive sense and getting a negative number. You need to call yourself on those.
In 1.c, you should do comparisons with things that make your life easier, not a mess. Compare with 1/x. Watch your vocabulary, too: 1/x doesn't diverge -- it's the integral.
- I checked on Problem 2, and only 10 our of 24 knew the formula for the area under a polar curve. Why not?
- 3.a: what does "exact" mean to you?
I mentioned this problem in class during our review. The question was whether one has to compute Simpson's by first computing LRR, RRR, Trap, and Mid. I told you that one doesn't have to, but that I might ask you to, and only give you the Simpson's (but expect you to compute the related rules). Many of you did too much work, since
for the other methods to generate
.
Discussion of the errors boils down to size and sign. We know what to expect, and the errors are consistent with that.
- This one requires the trick of
and
- Problem 5 was from section 8.1, and straightforward.
Except that a bunch of you didn't remember the formula for arc length of a curve given by y(x); or how to find the endpoints of the integral (the trip is over when the prey hits the ground, at y=0).
- Problem 6 is straight from the calculus with parametric
curves section 10.2, Example 5, p. 673.
If 6 was hard, it's because some of you didn't remember the role of r in the cycloid. It's the radius of the circle that traces it out. Some of you interpreted r as a function. That definitely complicates things.
- My god, the dx-droppers outnumber those who don't!
- concerns several different means of testing for convergence of
series with all positive terms (obviously, if we're dealing with series
of all negative terms, similar results are going to apply).
- We're not so concerned with the actual limits (that is the values
of the series) as we are with the convergence (or divergence) of the
series.
- Theorems:

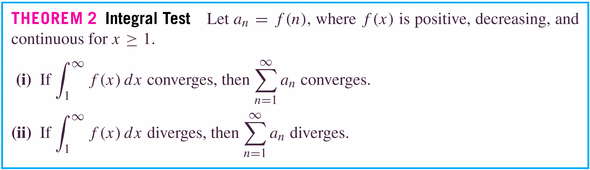
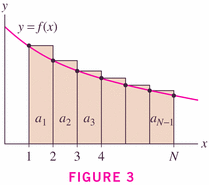
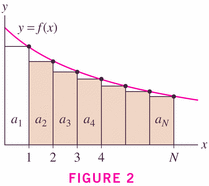
Theorem 3 is just a corollary of Theorem 2, where the integrals are the obvious power functions:

Let
, where f is a positive, decreasing function. If
converges by the integral test, and we define the remainder by
, then
(this gives us a bound on the error we're making in the calculation of a series). This is useful, for example, in the calculation of digits of
(now, you might ask "and what's the use of that?!";).
We can use this remainder inequality to get a bound on the true value of the series, just by adding
to each part of the inequality:
- Examples:
- We can use this method to demonstrate conclusively that the harmonic series is non-convergent.
- Dominoes (here's my page) -- and here's a more elegant page in Mathematica: Divergence of the harmonic series (and dominoes!)
- #22
- #36
- Theorems:
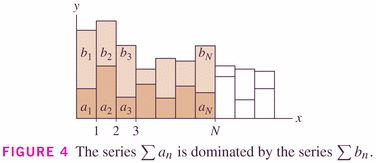
- if the series of the
if finite, so is the smaller series of
;
- if the series of the
if infinite, so is the larger series of
.
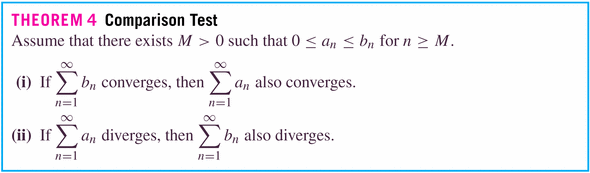
- geometric series, and
- p series, including
- the harmonic series (to show divergence).

This theorem says that, in the long run, one series has terms which are simply a constant times the terms in the other series.
In "the long run" means that we only really need to worry about the "tails" of series: we can throw away any finite number of terms for issues of convergence.
- if the series of the
- Examples:
- #6, p. 750
- #16
- #28
- #34 (draw a picture)
- #46
-
Once again, our mission here is not necessarily the value of the
series, but may be simply knowledge of whether it converges or
not.
- How does the author of this image reach the conclusion that "the sum is positive and at most
"?
- How about the partial sums --
-- what are they doing?
- What are the even partial sums doing?
- What are the odd partial sums doing?
- Examples:
- The alternating harmonic series is convergent
(Example 1, p. 753).
We need to show that the terms
of the series satisfy the Leibniz test:
- the terms are positive,
- the terms are decreasing in size,
- the terms have limit of 0.
- #5, p. 755
Identify the terms
, and decide whether they satisfy the Leibniz test.
- #13
- #17
Remember that for convergence, the conditions of the test need be true only eventually: convergence is all about the tail, not the head of the sequence.
- #23
For this one, we need the "Alternating Series Estimation Theorem" (p. 754):
- #27
- #34
- The alternating harmonic series is convergent
(Example 1, p. 753).
That being said, a theorem below does give us some help in determining the value of (or at least bounds on the value of) the series of a type called an "alternating" series. In particular, we want to look at alternating series like the one below:
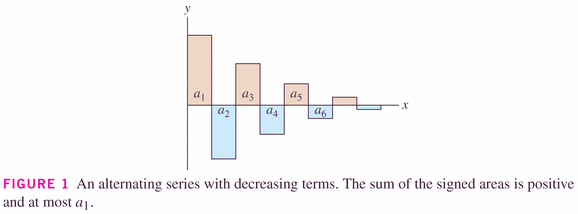
So it turns out that if the terms are converging to 0, then the alternating sequence converges to a limit.
Now we usually write our alternating series in the following way, illustrated by Leibniz's test: we assume that the are positive, and the term
takes care of the "alternation". (Our textbook switches to
for the positive part of the term.)

Our textbook calls this the "Alternating Series Test" (p. 751). The "Furthermore" part our textbook calls the "Alternating Series Estimation Theorem" (p. 754).