Day 39 in MAT229

Today:

• Announcements:
  • Your Section 11.2 homework is returned:
    • 16 -- part a; i and j are equivalent dummy indices; in part b, is independent of i, and hence constant. The second sum is thus
    • 20 -- this is a geometric series; compute c and r.
    • 44 -- You're supposed to use the fact that the series "telescopes". If you didn't, why not?

• Section 11.3: The Integral Test
  • concerns several different means of testing for convergence of series with all positive terms (obviously, if we're dealing with series of all negative terms, similar results are going to apply).

  • We're not so concerned with the actual limits (that is the values of the series) as we are with the convergence (or divergence) of the series.

  • Theorems:

    

    

    

    

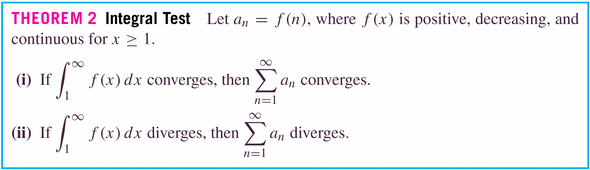
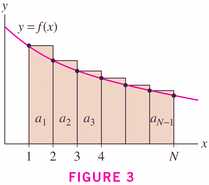
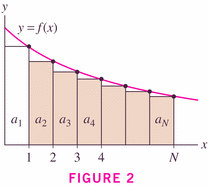
    Theorem 3 is just a corollary of Theorem 2, where the integrals are the obvious power functions:

    

    Let , where f is a positive, decreasing function. If converges by the integral test, and we define the remainder by , then

    

    (this gives us a bound on the error we're making in the calculation of a series). This is useful, for example, in the calculation of digits of (now, you might ask "and what's the use of that?!";).

    We can use this remainder inequality to get a bound on the true value of the series, just by adding to each part of the inequality:

    

  • Examples:
    • We can use this method to demonstrate conclusively that the harmonic series is non-convergent.
    • Dominoes (here's my page) -- and here's a more elegant page in Mathematica: Divergence of the harmonic series (and dominoes!)
    • #22
    • #36

• Section 11.4: Comparison Tests

  • Theorems:

    

    Notice how we can use each series to inform us about the other:
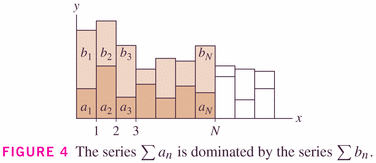
    1. if the series of the if finite, so is the smaller series of ;
    2. if the series of the if infinite, so is the larger series of .

    

    This comparison means that we'll need some series in our tool box with which to compare other series. The two obvious candidates are
    1. geometric series, and
    2. p series, including
    3. the harmonic series (to show divergence).
    But once we have a known series, we can throw it into our toolbox, too!

    

    This theorem says that, in the long run, one series has terms which are simply a constant times the terms in the other series.

    In "the long run" means that we only really need to worry about the "tails" of series: we can throw away any finite number of terms for issues of convergence.

  • Examples:
    • #6, p. 750
    • #16
    • #28
    • #34 (draw a picture)
    • #46 (this is a cool argument -- pay attention!)

• Section 11.5: Alternating Series
  Once again, our mission here is not necessarily the value of the series, but may be simply knowledge of whether it converges or not.

  That being said, a theorem below does give us some help in determining the value of (or at least bounds on the value of) the series of a type called an "alternating" series. In particular, we want to look at alternating series like the one below:

  

  1. How does the author of this image reach the conclusion that "the sum is positive and at most "?

  2. How about the partial sums -- -- what are they doing?

  3. What are the even partial sums doing?
  4. What are the odd partial sums doing?

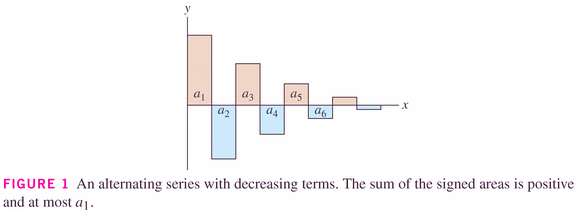
  So it turns out that if the terms are converging to 0, then the alternating sequence converges to a limit.

  Now we usually write our alternating series in the following way, illustrated by Leibniz's test: we assume that the are positive, and the term takes care of the "alternation". (Our textbook switches to for the positive part of the term.)

  

  Our textbook calls this the "Alternating Series Test" (p. 751). The "Furthermore" part our textbook calls the "Alternating Series Estimation Theorem" (p. 754).

  • Examples:
    • The alternating harmonic series is convergent (Example 1, p. 753).

      We need to show that the terms of the series satisfy the Leibniz test:

      1. the terms are positive,
      2. the terms are decreasing in size,
      3. the terms have limit of 0.

    • #5, p. 755

      Identify the terms , and decide whether they satisfy the Leibniz test.

    • #13
    • #17

      Remember that for convergence, the conditions of the test need be true only eventually: convergence is all about the tail, not the head of the sequence.

    • #23

      For this one, we need the "Alternating Series Estimation Theorem" (p. 754):

    • #27
    • #34